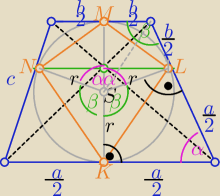
Pole trapezu równoramiennego ABCD wynosi 60. mm: Pole trapezu równoramiennego ABCD wynosi 60. W ten trapez wpisano okrąg o środku O i promieniu równym 3. Oblicz pole czworokąta KLMN, którego wierzchołkami są punkty styczności okręgu wpisanego w trapez ABCD z bokami tego trapezu (zobacz rysunek). Zapisz obliczenia

X: https://www.google.com/url?sa=t&source=web&rct=j&opi=89978449&url=https://studyx.ai/questions/4lsumng/zadanie-9-pole-trapezu-r-wnoramiennego-abcd-wynosi-60-w-ten-trapez-wpisano-okr-g-o-rodku&ved=2ahUKEwjRioTyrYeNAxVSKhAIHehbO_QQFnoECCIQAQ&usg=AOvVaw3T_dNWqKp2lBFZ6mKGVdhE

Misia: Inne rozwiązanie niż w linku podanym przez X 1/ sposób

	a+b
h=2r=6		*2r=60 ⇒ a+b=20 to c=10
	2

	2r		3		3
sinα=		=		i sinβ= sinα=		bo ( α+β=180o
	c		5		5

	1
PKLMN= 4* PΔKLS= 4*		*r*r*sinα
	2

P_KLMN= 10,8 ========== 2 \ sposób

	a		b
a+b=20 i r2=		*		⇒ ab=4r2 = 36
	2		2

Odcinek NL ma długość równą średniej harmonicznej długości podstaw trapezu ( można to wykazać)

	2ab		72
więc |NL|=		=
	a+b		20

	1
to PKLMN=		*2r*|NL|
	2

P_KLMN= 10,8 =============