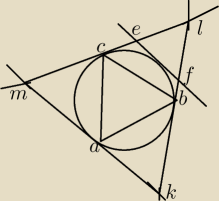
 Na trójkącie ostrokątnym ABC, w którym C = 45 stopni, a przeciwległy bok ma długość 3, opisano
okrąg. Styczne do okręgu w punktach A, B i C przecinają się w punktach K, L i M. Prosta
styczna do okręgu przecina dwa boki trójkąta KLM w punktach E i F. Oblicz pole trójkąta KLM,
jeśli wiadomo, że obwód trójkąta EFL jest równy 16 oraz |KM| = 7
Czy kąt przy wierzchołku K będzie równy 90 stopni?
Na trójkącie ostrokątnym ABC, w którym C = 45 stopni, a przeciwległy bok ma długość 3, opisano
okrąg. Styczne do okręgu w punktach A, B i C przecinają się w punktach K, L i M. Prosta
styczna do okręgu przecina dwa boki trójkąta KLM w punktach E i F. Oblicz pole trójkąta KLM,
jeśli wiadomo, że obwód trójkąta EFL jest równy 16 oraz |KM| = 7
Czy kąt przy wierzchołku K będzie równy 90 stopni?
| 3√2 | ||
jest kwadratem o boku równym | ||
| 2 |
| 21√2 | 147√2 + 126 | |||
21√2 = x(14 − 6√2) −−−> x = |LB| = | = | |||
| 14 − 6√2 | 62 |
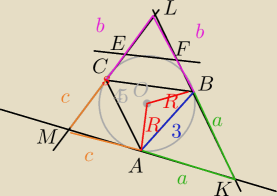 Potwierdzam wersję wredulusa
Potwierdzam wersję wredulusa  <AOB = 90
3 = R√2
<AOB = 90
3 = R√2
| 3√2 | ||
R = | ||
| 2 |
| 3√2 | 3√2 | |||
72 + (b+ | )2 = (7− | +b)2 | ||
| 2 | 2 |
| 1 | 3√2 | |||
P(KLM) = | *7*( | +b) | ||
| 2 | 2 |