trójkat 123: Dany jest trójkąt prostokątny równoramienny ABC, gdzie ∡ BAC=90^o i AB=AC=7. Wybrano trzy punkty D,E,F odpowiednio na bokach BC,CA,AB tak, że ∡EDF=90^o, DE=5, DF=3. Oblicz długość BD.

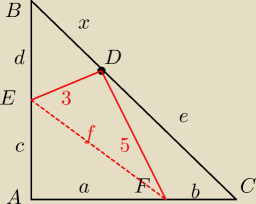
wredulus_pospolitus: pierwsze co widzę:

⎧	a+b = 7
⎜	c+d=7
⎜	x+e=7√2
⎨	f2=32+52
⎜	a2+c2=f2
⎜	9=d2+x2−dx√2
⎩	25=b2+e2−be√2

siedem równań ... siedem niewiadomych

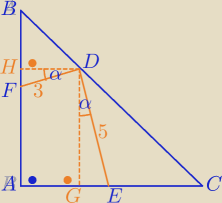ite: |BC|=|BD|+|DC|=7√2 |HD|*√2=|BD|, |DG|*√2=|DC|

	|HD|		|DG|
ΔHDF∼ΔGDE →		=
	3		5

|BD|/√2		|DC|/√2		|BD|*5
	=		→ |DC|=
3		5		3

	|BD|*5
|BD|+		=7√2
	3

	21√2
|BD|=
	8

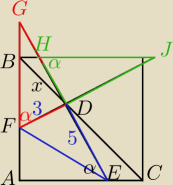an: Trójkąty BHD i ECD są podobne. Trójkąty DHJ i DFG są przystające tym samym: FD=DH=3 BC=7√2 DC=BC−x =7√2−x

5		7√2−x
	=
3		x

	21√2
x=
	8

lyly19: Bardzo ciekawe i klasyczne zadanie geometryczne! https://retrobowl25.com

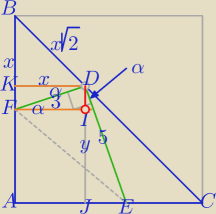Mila: y=7−x ΔFKD∼ΔEJD

x		7−x
	=
3		5

5x=21−3x

	21
x=
	8

	21√2
|BD|=
	8

To samo co u ite, ale trochę krócej.

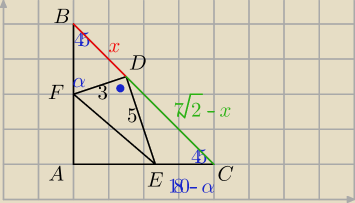SAIzou: To ja dorzucę tw. sinusów do rozwiązań

x		3
	=
sinα		sin45

7√2−x		5
	=
sin(180−α		sin45

....

	21√2
x =
	8