Tangens
Miś Uszaty:
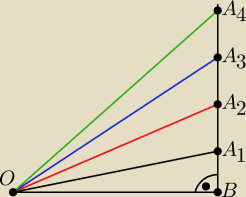
Na rysunku bedzie
∡BOA
1=∡A
1OA
2=∡A
2OA
3=∡A
3OA
4
Opierając sie na własnościach dwusiecznej w trójkącie zbadac która z dwóch liczb jest większa
1) tg2α czy 2tgα
2) tg3α czy 3tgα
3) tg3α czy tg2α+tgα
Czy wobec tego tangens rośnie proporcjonalnie do kąta ?
15 kwi 22:40
Miś Uszaty:
Jeszcze jest jedno polecenie do tego rysunku
Zbadac która z liczb jest większa
15 kwi 22:47
Miś Uszaty:
16 kwi 09:45
Uszatek:
"będzie"?, na rysunku "jest"
16 kwi 10:21
. :
Z oczywistych oczywistości mamy:
|A
4O| > |A
3O| > |A
2O| > |A
1O|
Mając to na uwadze i biorąc po uwagę Tw. O dwusiecznej wychodzi nam:
|A
4A
3| > |A
3A
2| > |A
2A
1|
Zwiazku z tym
| | |A3A2| + |A2A1| | | 2*|A2A1| | |
tg(2a) = |
| > |
| = 2tga |
| | |OA1| | | |OA1| | |
Analogicznie szacujemy w pozostałych podpunktach
16 kwi 10:45
. :
Trochę powaliłem oznaczenia... Skończyłem na A
1 a nie na B
16 kwi 10:56
Miś Uszaty: dobrze
16 kwi 15:13
. :
A co do ctg'sow to zauwaz
| | 1 | |
ctg(2a) = |
| < {1}{2tga} = 1/2 * ctga |
| | tg(2a) | |
16 kwi 17:22