optymalizacja witamimasakra: Na przedziale [−7,2] określono dwie funkcje f(x)=√4x+28 i g(x)=−√x+7. Rozpatrujemy wszystkie trapezy ABCD, których wierzchołki A i D leżą na wykresie funkcji f, a wierzchołki B i C leżą na wykresie funkcji g. Podstawy rozpatrywanych trapezów są równoległe do osi Oy i |AB|<|CD|. Wykaż, że jeżeli druga współrzędna punktu B jest równa (−y) to pole trapezu ABCD jest nie większe niż P(y)=−3/2(y³+3y²−9y−27).

kubuspuchatek: Rowniez mam problem z tym zadankiem Jak ktos by mogl pomoc bylbym wdzieczny https://zadania.info/d1861/65508 tutaj link, zadanie nr 13

M:

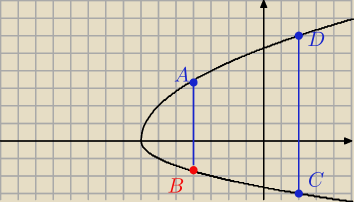wredulus_pospolitus: 0. Rysunek oraz f(x) = √4x+28 = 2√x+7 1. Zauważmy (to nie koniecznie, ale co mi tam), że: y³ + 3y² −9y − 27 = y(y² − 9) + 3(y² − 9) = (y²−9)*(y+3) 2. Mamy wykazać, że pole jest nie większe niż P(y). 'Nic' nie wiemy o punktach D i C (poza tym, że |DC| > |AB|), związku z tym przyjmujemy, że x_D = x_C = 2 (czyli |DC| będzie przyjmowała największą możliwą wartość, czyli rozpatrujemy trapezy o największym polu) Związku z tym |CD| = f(2) − g(2) = 2*3 − (−3) = 9 3. Punkt B ma współrzędne (x_B , y_B). Uzależniamy x_B od y_B y_B = −√x_B + 7 −−−> −y_B = √x_B + 7 //² −−−> (y_B)² = (x_B + 7) −−−> −−−> x_B = (y_B)² − 7 4. wyliczamy |AB| |AB| = f(x_B) − g(x_B) = 3√x_B+7 = 3√y_B² = 3(−y_B) zastanówcie się dlaczego tu jest minus Najważniejsza rzecz (na której pewnie 90% poległa ) w zadaniu mamy podane: y_B = −y stąd: |AB| = 3(−(−y) = 3y 5. oraz h h = 2 − x = 2 − (y² − 7) = 9 − y² 6. Podstawiamy do wzoru na pole trapezu:

	|AB| + |CD|		3(y + 3)		3
P =		*h =		*(9−y2) = −		*(y+3)(y2−9)
	2		2		2

7. I teraz wystarczy komentarz odnośnie (2.), że dla innych x_D pole trapezu będzie mniejsze, bo |CD| < 9 oraz h < 9 − y²

wredulus_pospolitus: PS. Jeżeli ktoś przez nieuwagę, nie zauważył, że y_B = −y tylko odruchowo podstawił y_b = y to wyszło mu |AB| + |CD| = 3(3 − y) Jeżeli nieuważny uczeń zrobiłby (1.) to by widział że tenże 'minus' tu mi nie pasuje i miałby szansę odnaleźć swój błąd ... bez tego, ciężko by było to uczynić.