dowód 123: Niech ABC będzie trójkątem ostrokątnym o wysokościach AD, BE, CF. Wykaż ze Pole_DEF = (sin²A * sin²B + sin²C−2) * Pole_ABC

M:

M:

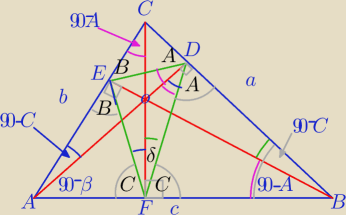
Mila: 1) Na czworokątach: AFOE,BFOD, CDOE można opisać okręgi. 2)

	π
∡F=2*(		−C)=π−2C
	2

analogicznie : ∡D=π−2A ∡E=π−2B ============ 3) Trójkąty: AFE, BFD, CED są podobne do ΔABC. Na rysunku :

	π
δ=		−C to ∡DFB=C
	2

Podobnie w pozostałych przypadkach. 4)

	AE
ΔAFE∼ΔABC w skali ka=		=cosA
	c

	DB
ΔBFD∼ΔABC w skali kb=		=cosB
	c

	CD
ΔCED ∼CED w skali kc=		=cosC
	b

5) P − pole ΔABC P_DEF=P−(cos²A*P+cos²B*P+cos^c*P)= =P*(1−(cos²A+cos^B+cos^C) )= P_DEF=(sin²A+sin²B+sin²C−2)*P ============================

Mila: Poprawiam zapis: P_DEF=P−(cos²A*P+cos²B*P+cos²C*P)= =P*(1−(cos²A+cos²B+cos²C) )

Mila: Inny wzór na pole ΔDEF: 1) DF=b*cosB, EF=a*cosA, DE=c*cosC

	FE*FD
PDEF=		* sin2C= a cosA*b*cosB*sinC*cosC
	2

P_DEF=ab cosA* cosB *cosC* sinC