Styczne i okręgi
Miś Uszatek:
Mam kilka takich konstrukcyjnych zadań z okręgiem
Zadanie nr 1
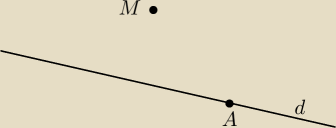
Przez dany punkt M nie leżący na danej prostej d poprowadzic okrąg styczny do niej w danym
punkcie A
próbowałem wykreślic prostopadłe ale nie stykał mi sie z punktem A
2 kwi 23:50
Miś Uszatek:
Zadanie nr 2
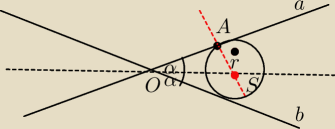
Dane sa dwie proste a i b przecinające sie w punkcie O
Przez punkt A prostej a rózny od O poprowadzić okrąg styczny do obu prostych
Rysuje dwusieczną kąta aOb
Rysuje prosta prostopadła do a i przechodząca przez A która przetnie dwusieczna w punkcie S
Dlugośc odcinka SA to promien tego okregu
A jak bedziemy mieli dany promien i poprowadzic okrąg o danym promieniu do dwóch przecinających
sie prostych a i b ?
3 kwi 00:11
Mila:
1) Symetralna AM.
2) a − prostopadła do prostej d i przechodząca przez punkt A .
3) środek szukanego okręgu leży w punkcie przecięcia prostych AM i a.
Powodzenia
3 kwi 00:14
Mila:
3) środek szukanego okręgu leży w punkcie przecięcia prostych: symetralnej AM i a.
3 kwi 00:17
Miś Uszatek:
Dziękuje
.
Nastepne zadanie jest takie
Poprowadzić wspólna styczną do dwóch danych okęgów
To juz sobie zrobie .
3 kwi 00:18
Miś Uszatek:
Milu
Zrobiłem rysunek do postu z 00 : 17 i ten okrąg nie bedzie styczny do prostej a w punkcie A
Bedzie przechodził przez punkty A i M
5 kwi 16:37
Mila:
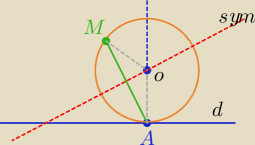
Rys. do zadania z 23: 50
6 kwi 01:27
Mila:
To chyba nieporozumienie wynikające z oznaczeń.
okrąg jest styczny do prostej d w punkcie A.
a− prosta ⊥d
6 kwi 01:31
Miś Uszatek:
Milu
Tak własnie zrobiłem
Odczytałem to że punkt przecięcia symetralnej z prosta d
Najwazniejsze że wyjasnione .Pozdrawiam
6 kwi 01:45
Mila:
6 kwi 18:43