Planimetria - prostokat Kamilox: Dany jest prostokat ABCD w ktorym AB=4 i BC=2. Punkt E jest srodkiem boku BC. Na odcinku DE wyznaczamy punkt F taki, ze EF = BE. Prosta prostopadla do DE przechodzaca przez punkt F przecina bok AB w punkcie G. Oblicz dlugosc odcinka FG.

Kamilox:

wredulus_pospolitus: 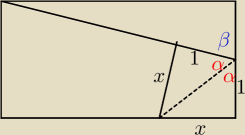β = 180−2α

	2tgαα		2x
8 = tgβ = tg(180 − 2α) = −tg(2α) =		=
	tg2α − 1		x2−1

więc masz do rozwiązania: 8x² − 2x − 8 = 0

Kamil: Skąd wiemy że dwa kąty α są takie same. Tgβ nie powinien być równy 4? Bo many 4/1; CD/EC

wredulus_pospolitus: prawda ... 4. Co do kątów −−− masz tw. Pitagorasa przy dwóch bokach o tej samej długości daje taką samą długość trzeciego boku (x) ... co dalej daje Ci przystawanie (BKB)

Kamilox: Ok. A da się jakoś bez użycia wzoru na tg podwójnego kata?

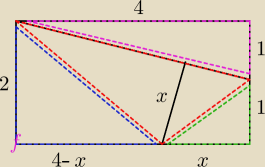
wredulus_pospolitus: Zliczamy pola:

	4*1		x*1		x*√5		(4−x)*2
4*2 =		+		+		+
	2		2		2		2

16 = 4 + x + x√5 + 8 − 2x jedyne co musisz jeszcze wcześniej policzyć (a ja zrobiłem to w pamięci), to policzyć podstawę czerwonego trójkąta

chichi:

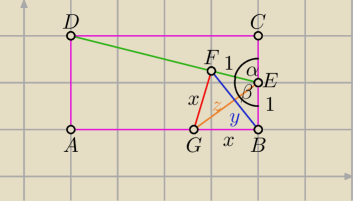
	1		1
1) cos(α) =		⇒ cos(β) = −
	√17		√17

	1
2) tw. Carnota w ΔFEB: y2 = 1 + 1 − 2*1*1*(−		) ⇒ y = √2+(2√17)/17
	√17

3) x² + 1² = z² ⇒ z = √1 + x² 4) EFGB jest deltoidem, zatem P = 0.5zy = 0.5√(1 + x²)(2+(2√17)/17) = 2 * 0.5 * 1 * x

	1 + √17
rozwiązując to równanie otrzymasz x =		.
	4

Czy jest to szybsze rozwiązanie? Zapewne nie, ale nie jest też długie. Nie korzysta przy tym z tangensa podwojonego kąta − tak jak chciałeś, możesz sprawdzić czy wyniki się pokrywają, o ile nie kopnąłem się w rachunkach

chichi: @wredulus w pitagorasie jest suma kwadratów długości przyprostokątnych, a nie suma długości przyprostokątnych