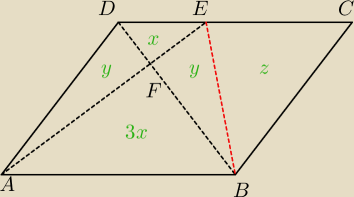
Geometria Razor: Dany jest rownoleglobok ABCD. Punkt E leży na boku CD a punkt F na przecieciu odcinkow BD i AE. Pola trojkatow ABF i EDF wynosza odpowiednio 3 i 1. Oblicz pole trojkata BCE.

wredulus_pospolitus:

	1
1. Zauważamy, że PΔABD = PΔBCD =		P▱ABCD
	2

2. Rysujemy BE. 3. Zauważamy, że ABED to trapez, stąd P_ΔAFD = P_ΔBFE 4. Oznaczamy 'pola' trójkątów i układamy równanie: z + x+y = y + 3x −−−> z = 2x Więc P_ΔBCE = 2*P_ΔDEF

wredulus_pospolitus: ach ... x = 1 ja myślałem, że stosunek ich pól jest 3 : 1 ... no ale po za tym, że otrzymamy konkretną wartość ... to nic nie zmienia w samych obliczeniach.

Razor: Dzieki. Zastanawiam się tylko z czego wynika ze ΔAFD = ΔBFE.

wredulus_pospolitus: Rozor: P_ADE = P_AFD + P_DFE P_BDE = P_BFE + P_DFE natomiast ΔADE i Δ BDE mają taką samą podstawę (DE) i wysokość (h_trapezu) więc mają równe pola. Więc ΔAFD i ΔBFE także mają równe pola

Razor: Wszystko już rozumiem. Dzięki wielkie!

wredulus_pospolitus: @Razor −−− warto sobie zapamiętać ten fakt ... dotyczy to każdego trapezu.