Planimetria - okręgi
Kamilox: Na okręgu O1 wybrano punkty S, A i B.
Okrąg O2 o środku S i promieniu SA przecina okrąg O1 w punktach A i C.
Prosta AB przecina okrąg O2 w punktach A i D.
Udowodnij, że trójkąt BCD jest równoramienny.
31 mar 23:59
wredulus_pospolitus:
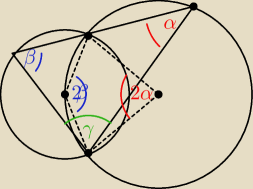niebieskie i
czerwone kąty na jakiej podstawie
Na tej samej podstawie mamy:
2*2β = (360−2α)
a tego mamy: 2*(2β + α) = 360 −−−> 2β + α = 180
o −−−>
γ = β −−> mamy trójkąt
równoramienny
1 kwi 00:46
Kamilox: Nie bardzo rozumiem z czego wynika to, ze:
2*2β = (360−2α)
1 kwi 13:01
wredulus_pospolitus:
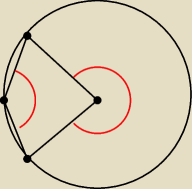
patrz na te dwa kąty
1 kwi 13:10
Razor: Dzięki. Rozumiem
2 kwi 00:20