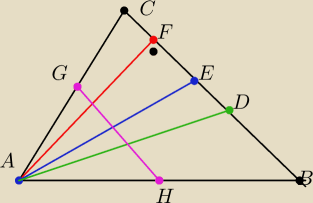
Trójkąt rożnoboczny Podstawy Geometrii: W trójkącie ABC różnobocznym z wierzchołka A wykreślono dwusieczną kąta A ,oraz środkową i wysokość względem boku BC Udowodnić że odcinek łączący środki boków AB i AC dzieli dwusieczną środkowa i wysokość na połowy Wskazówka : Rozpatrzcie kolejno trójkaty których jednym bokiem będzie a) dwusieczna AD b) środkowa AE c) wysokośc AF W trójkącie ABC GH jest linią środkową tego trójkąta więc jest równoległa do boku BC Rozpatrzmy więc trójkaty AFC, AEC i ADC Korzystając z twierdzenia prostego: Jeżeli na jednym ramieniu kąta odłożymy kilka równych odcinkow i przez punkty podziału wykreslimy proste do siebie równoległe to te proste wyznaczą na drugim ranieniu kąta odcinki równe miedzy sobą Stąd linia GH dzieli kazdy z odcinków AD,AE,AF na równe dwa odcinki

wredulus_pospolitus: jedna kwestia −−− to twierdzenie (szczerze, pierwsze o tym słyszę) to nic innego jak wniosek z tw. Talesa

Podstawy Geometrii: https://zapodaj.net/plik-cUfM3eCUoj Dalej jest Podstawiając zamiast BK i DL równe im odcinki CE i EF otrzymamy AC=CE=EF co należało udowodnic