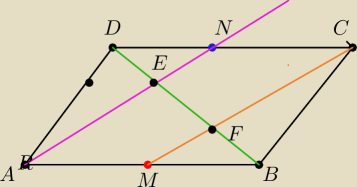
 Dany jest równoległobok ABCD
Oznaczmy odpowiednio przez M i N odpowiednio środki boków AB i CD.
Udowodnić że proste AN i CM dzielą przekątną BD na trzy równe odcinki oraz przekątna BD
przecina prostą AN
w punkcie którego odległośc od A jest dwa razy większa niż od punktu N
Trójkat ADN ≡trojkata MBC na podstawie cechy bok,bok bok
Stąd DE=FB
Na razie tylko tyle wymysliłem
Dany jest równoległobok ABCD
Oznaczmy odpowiednio przez M i N odpowiednio środki boków AB i CD.
Udowodnić że proste AN i CM dzielą przekątną BD na trzy równe odcinki oraz przekątna BD
przecina prostą AN
w punkcie którego odległośc od A jest dwa razy większa niż od punktu N
Trójkat ADN ≡trojkata MBC na podstawie cechy bok,bok bok
Stąd DE=FB
Na razie tylko tyle wymysliłem
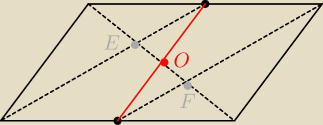 1. Rysujemy MN.
2. Zauważamy że wszystkie cztery trójkąty: ADN , NMA , MNC , CBM są przystające.
3. Zauważamy, że ΔAED podobny do ΔNEO −> skala =
1. Rysujemy MN.
2. Zauważamy że wszystkie cztery trójkąty: ADN , NMA , MNC , CBM są przystające.
3. Zauważamy, że ΔAED podobny do ΔNEO −> skala =  −−−> stąd |EO| =
−−−> stąd |EO| =  *|DE|
a także |NE| =
*|DE|
a także |NE| =  *|AN|
4. Zauważamy, że trójkąty NDE i MFO są przystające, stąd |EF| = |DE| (= |FC|)
*|AN|
4. Zauważamy, że trójkąty NDE i MFO są przystające, stąd |EF| = |DE| (= |FC|)
| 1 | ||
przed punktem 3 jeszcze trza wykazać, że |NE| = | |AD| .... najprościej z podobieństwa | |
| 2 |