 PROSZĘ O SPRAWDZENIE i ewentualne poprawienie...
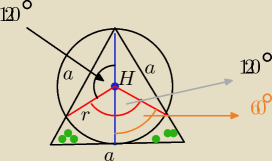
Wysokość trójkąta równobocznego T jest średnicą koła K. Oblicz pole tej części trójkąta T,
która nie zawiera się w kole K.
Pszukane = Ptrójkąta równobocznego − 2 (Pwycinka koła + Ptrójkąta rozwartokątnego)
PROSZĘ O SPRAWDZENIE i ewentualne poprawienie...
Wysokość trójkąta równobocznego T jest średnicą koła K. Oblicz pole tej części trójkąta T,
która nie zawiera się w kole K.
Pszukane = Ptrójkąta równobocznego − 2 (Pwycinka koła + Ptrójkąta rozwartokątnego)
| a2 √3 | ||
Ptrójkąta równobocznego = | ||
| 4 |
| a √3 | 1 | a √3 | ||||
H = | r = | H = | ||||
| 2 | 2 | 4 |
| α | ||
Pwycinka koła = | * πr2 α = 60 | |
| 360 |
| 1 | a √3 | a2 π | ||||
Pwycinka koła = | * π * ( | )2 = | ||||
| 6 | 4 | 32 |
| 1 | 1 | |||
Ptrójkąta rozwartokątnego = | * (r * | H * sin β) β = 120 | ||
| 2 | 2 |
| 1 | a √3 | 1 | a √3 | |||||
Ptrójkąta rozwartokątnego = | * | * | * | * sin 120 | ||||
| 2 | 4 | 2 | 2 |
| 3a2 | √3 | |||
Ptrójkąta rozwartokątnego = | * | ? | ||
| 32 | 2 |
| 3a2 √3 | ||
Ptrójkąta rozwartokątnego = | ||
| 64 |
| a2 √3 | 3a2 √3 | a2 π | ||||
Pszukane = | − 2 ( | + | = | |||
| 4 | 64 | 32 |
| a2 √3 | 3a2 √3 + 2a2 π | |||
= | − 2 ( | ) = | ||
| 4 | 64 |
| a2 √3 | 3a2 √3 + 2a2 π | |||
= | − | = | ||
| 4 | 32 |
| 8a2 √3 − 3a2 √3 + 2a2 π | 5a2 √3 + 2a2 π | |||
= | = | |||
| 32 | 32 |
