odcinek i punkt
Podstawy Geometrii:
Na danym odcinku AB wyznaczyc punkt którego odległośc od danego punktu P płaszczyzny jest
a) najmniejsza
b) największa
Rozpatrzyc rozmaite przypadki zależnie od połozenia punktu P względem podcinka AB
29 mar 18:30
wredulus_pospolitus:
ten punkt P to jest dowolny punkt na płaszczyźnie? Czy jest to konkretnie ustalony punkt?
29 mar 18:37
Podstawy Geometrii:
Według mnie to dowolny punkt płaszczyzny
29 mar 18:39
Podstawy Geometrii:
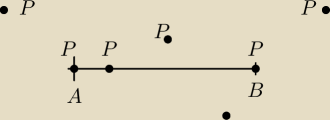
Moze to być tak
29 mar 18:42
wredulus_pospolitus:
to może inaczej ... jesteś w 2D czy w 3D
Bo ja założyłem początkowo że w 3D
29 mar 18:51
wredulus_pospolitus:
Jeżeli w 2D to:
0. Jeżeli punkt P leży na odcinku AB to P jest tym punktem.
1. Z punktu P rysujemy prostą prostopadłą do prostej zawierającej AB, jeżeli prostopadła:
a. przecina odcinek AB, to punkt przecięcia jest tym punktem.
b. nie przecina odcinka AB to koniec odcinka, który jest 'bliżej' przecięcia prostych, jest
tymże punktem.
29 mar 18:54
wredulus_pospolitus:
Największa:
Zawsze to będzie któryś z końców odcinka AB.
W zależności gdzie przecinają się proste, będzie to ten 'dalej od przecięcia'.
29 mar 18:55
Podstawy Geometrii:
Może tak .
Jestem w 1973 roku
29 mar 19:17
29 mar 19:25
Podstawy Geometrii:
NIe ma rozwiązania i tak
29 mar 19:36
29 mar 19:43
Podstawy Geometrii:
Dziękuje za cięzką prace
29 mar 19:45
Podstawy Geometrii:
Czy to zadanie kiedyś wstawiałem bo już nie pamiętam
Dwa okręgi
C(O1,r1) i C(O2,r2) przecinają się w punktach M i N
Oznaczmy przez P punkt pierwszego okręgu różny od M leżący na średnicy O1M i przez Q (Q≠M)
punkt drugiego okręgu leżący na średnicy O1N.
Udowodnić ze punkty P,N Q są współliniowe ,oraz że PQ=2O1O2
29 mar 20:23
wredulus_pospolitus:
Sprawdź treść zadania ... to co napisałeś nie ma sensu
29 mar 20:29
wredulus_pospolitus:
to chyba miało być −−−> Q leży na średnicy
O2M , prawda
29 mar 20:34
Podstawy Geometrii:
W zadaniu jest O2N (przepraszam ) ale właśnie mi nie pasuje
29 mar 20:42
wredulus_pospolitus:
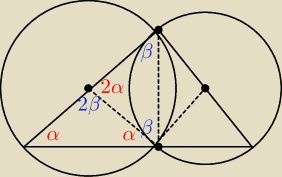
Co do pierwszej części: rysujesz promienie do punktu N oraz odcinek MN ... zauważasz trójkąty
równoramienne ... zaznaczasz kąty ... stąd dostajesz, że ∡PNM = ∡QNM = 90
o
Co do drugiej części ... zauważamy, że ΔPMQ jest prostokątny, natomiast ΔO
1MO
2 jest podobny
do niego ... skala =
I masz drugą część
29 mar 20:44
wredulus_pospolitus:
musi być O2M ... inaczej to nie ma sensu.
29 mar 20:45
29 mar 20:49
wredulus_pospolitus:
Ja nie twierdzę, że źle przepisałeś ... po prostu jest literówka w książce ... nawet w tych za
komuny się zdarzało.
29 mar 20:55
Podstawy Geometrii:
Będe to zaraz sobie ogarniał
Sliczne dzięki za pomoc
29 mar 20:55
wredulus_pospolitus:
A dlaczego musi być O2M:
1. Bo inaczej nie ma sensu zakładanie, że Q≠M
2. Zadanie jest błędne (wtedy Q i N leżą na tej samej średnicy, natomiast punkt P nie ma
absolutnie żadnej szansy leżeć na tej prostej zawierającej tą średnicę)
29 mar 20:57
Podstawy Geometrii:
Niestety tez juz trace wzrok i tez moge żle przepisać
Ksiązka to Geometria dla klasy 1 Witold Janowski
29 mar 20:58
29 mar 20:59
Podstawy Geometrii:
wredulus
πiesio to zapewne
Eta bo ona często się chwaliła że musi wyjśc na spacer z psem
Pozdrawiam
29 mar 21:06