trójkat Kamil: Dany jest trójkąt ABC o bokach AB = 20, AC = 8 i BC = 14. Niech CF będzie dwusieczną kąta C taką, że F leży na boku AB. Symetralna odcinka CF przecina BC w punkcie D i AC w punkcie E. Oblicz pole czworokąta AEDF?

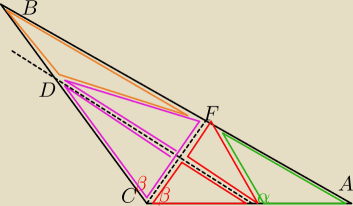
wredulus_pospolitus: UWAGA Rysunek 'nie jest w skali ' (faktycznie kąt przy C będzie o wiele bardziej bliski 180^o)

	80		140
0. Z tw. o dwusiecznej masz |AF| =		; |BF| =
	11		11

1. czerwone Δ są przystające (KBK) 2. Więc: α = 180 − 2*(90 − β) = 2β 3. Więc zielony Δ podobny do ΔABC −−−> |AE| = ... −−−> k = ... −−−> P_ΔAEF = .... 4. Analogicznie fioletowe Δ przystające (także KBK) 5. Więc pomarańczowy Δ podobny do ΔABC −−−> |DF| = ... −−−> k' = ... −−> P_ΔFDB = ... 6. W takim razie P_{deltoidu ECDF} = P_ΔABC − P_ΔADF − P_ΔFDB

	1
7. PΔEDF =		Pdeltoidu = ...
	2

8. P_AEDF = P_ΔAEF + P_ΔEDF = ... Kooooniec PS. Zastanów się jaki wzór zastosować na P_ΔABC w momencie gdy znamy długości jego boków

wredulus_pospolitus: Poprawka: przystawanie na podstawie BKB a nie KBK

wredulus_pospolitus: Poprawka 2: tak naprawdę |AE| i |DF| nie trzeba wyliczać ... to jest pozostałość z mojego pierwotnego podejścia do problemu

Mila: Pozdrawiam Artur, ładnie jest. Jeśli liczymy na ogólnych danych to obliczenia są mniej uciążliwe. Na końcu liczymy na konkretach pole Δ ABC i pole czworokąta.