Trapez Halinka: Pole trapezu ABCD o podstawach AB=16 i CD=12 wynosi 98. Punkt S jest punktem przeciecia przekatnych trapezu. . Oblicz pole trójkata ABS

wredulus_pospolitus: 1. Masz pole i masz długości podstaw −−−> masz wysokość 2. Zauważ, że w trójkąty ABS i CDS są PODOBNE układasz proporcję

hABS		16
	=		; pamiętając, że hCDS = htrapezu − hABS
hCDS		12

3. obliczasz pole trójkąta ABS

malinka:

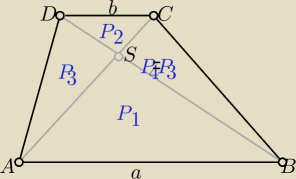
	a
ΔABS ∼Δ CDS w skali k =
	b

P−− pole trapezu P=(k+1)²*P₂ P₃=P₄=k*P₂ P₁=k²*P₂ to

	P		kP		k2P
P2=		P3=P4=		P1=
	(k+1)2		(k1)2		(k+1)2

	4
w tym zadaniu k=		i P= 98
	3

malinka: zapis ma być:

	kP
P3=P4=
	(k+1)2

Iryt:

	12+16
PABCD=		*h
	2

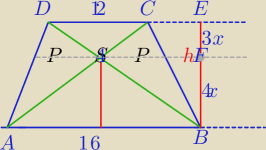
14h=98 h=7

	16		4
ΔABS∼ΔDCS w skali k=		=
	12		3

BF		4
	=
FE		3

7x=7 x=1, 4x=4

	16*4
PΔABS=		=32
	2