Mam takie zadanie Arnold: 1. W trapezie równoramiennym ABCD punkty styczności E oraz F okręgu wpisanego dzieli ramiona boczne AB oraz CD w stosunku 2:3 licząc od B oraz C. Promień okręgu wpisanego wynosi 3. Wyznacz a) pole trapezu b) pole koła opisanego na trapezie c) długość odcinka CE.

wredulus_pospolitus: "od B oraz C" chyb miało być "od D oraz C"

wredulus_pospolitus: rysunek nie oddaje proporcji 2:3, a przez to także innych proporcji. opuszczamy wysokość z D ... mamy trójkąt prostokątny z jedną niewiadomą (x) ... z Pitagorasa wyznaczamy wartość x. Mając to ... cała reszta to już kwestia obliczeń

Arnold: wkleiłem z tego co dostałem od nauczyciela. Są to zadania z zbioru maturalnego aksjomat ale nie jestem pewnien bo nie mam go fizycznie, ale polecenie jest takie jakie dostałem Możliwe że jest błąd..

wredulus_pospolitus: nie ... jest dobrze ... ja po prostu nie oznaczyłem ... trza zmienić rysunek

wredulus_pospolitus: w sensie ... tak oznaczyć wierzchołki

Arnold: czy mógłbyś mi pomóc z podpunktem b oraz c bo nie wiem co zrobić ?

Arnold: Wyszło mi x= √3/2

Fluu: A pole jest 30 √3/2

uuu:

	√6
x= √3/2=
	2

P= 30√3/2=15√6

Arnold: i co zrobić dalej w punktach b oraz c bo nie wiem?

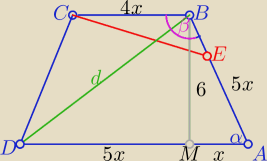
uuu: b) Oblicz wΔAMB sinα =... oblicz długość |DB|=d z tw. Pitagorasa w Δ DMB okrąg opisany na tym trapezie to ten sam co opisany na ΔDAB z tw. sinusów

	d
2R=		⇒ R=...
	sinα

P(koła opisanego)=πR²=....

uuu: c) z tw. cosinusów w Δ CEB |CE|²= |CB|²+|BE|²− 2CB*BE*cosβ gdzie cos β= cos(180^o−α)= − cosα cosα = √1−sin²α i licz........

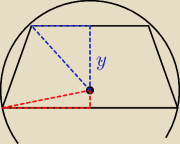
wredulus_pospolitus: 24x² = 36 −−−> x² = 1.5 (b) masz dwa trójkąty prostokątne o tej samej przekątnej ... stąd: (2x)² + y² = (3x)² + (6−y)² ( = R²) wyliczasz najpierw y, później R ... i masz pole