Podział proporcjonalny w trójkącie równoramiennym - dowód Marek: Czy jest takie twierdzenie, które mówi, że jeżeli w trójkącie równoramiennym, gdzie |AB|=|BC| poprowadzimy prostą z wierzchołka B, która przetnie nam podstawę AC w stosunku x/y to prosta ta podzieli też w takim samym stosunku kąt ABC?

Podstawy Geometrii: W trójkącie równoramiennym na pewno dwusieczna kąta B podzieli podstawe w stosunku 1 : 1 Co do reszty to zrobiłbym kilka rysunków i sprawdził

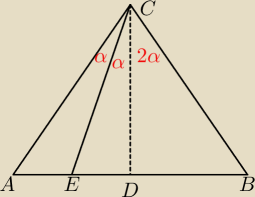
wredulus_pospolitus: Załóżmy że tak jest w takim razie przy podziale podstawy 1:3 mielibyśmy. Co oznacza, że w trójkącie prostokątnym ADC, środkowa (CE) jest dwusieczną kąta. A to natychmiast obalamy, ponieważ w takiej sytuacji niespełnione jest tw. o dwusiecznej:

|AC|		|CD|
	=		−−−−> |AC| = |CD|
|AE|		|ED|

Marek: Dziękuję za odpowiedzi, zrobiłem na przykładzie trójkąta równoramiennego o kącie między ramionami 120 i też nie wyszło: https://zapodaj.net/plik-bjzdV3mjsv Jakby się ktoś zastanawiał to w równobocznym również to nie działa: https://zapodaj.net/plik-HZgWhecYtn Moja teza okazała się fałszywa

wredulus_pospolitus: z żadnym nie będzie to działało jedyna sytuacja to w trójkącie równoramiennym poprowadzona środkowa dzieli także dzieli kąt na pół. Każda inna proporcja nie będzie spełniona co można dowiesz uogólniając to co pisałem o 11:56. I opierając się na tym, że dwusieczna kąta i środkowa pokrywają się ze sobą TYLKO w trójkącie równoramiennym.

w: i równobocznym

wredulus_pospolitus: @w − wskaż mi trójkąt równoboczny który NIE JEST trójkątem równoramiennym to tak jakbym napisał: "wszystkie prostokąty można wpisać w okrąg", a co Ty byś napisał: "i kwadraty też" zapominając, że kwadrat jest prostokątem