czy mógłby ktoś pomóc z tym zadaniem Reginald: . W czworościanie foremnym poprowadzono płaszczyznę przechodzącą przez wysokość podstawy i środek jednej z krawędzi bocznych. Pole tego przekroju wynosi P= 9 √11. Oblicz a) objętość czworościanu. b) stosunek objętości brył, na jakie płaszczyzna ta podzieliła wyjściowy czworościan.

wredulus_pospolitus:

	1
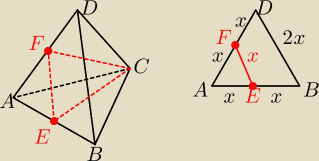
1. Z podobieństwa trójkątów / tw. cosinusów mamy |EF| =		|AB|
	2

2. Zauważmy, że FC jest wysokością trójkąta ADC ... związku z tym |FC| = |EC| = ... 3. W takim razie trójkąt CEF jest trójkątem równoramiennym, znamy jego boki ... mamy jego pole W takim razie jesteśmy w stanie wyliczyć 'x' 4. Stąd V_{czworościanu} = ... 5. Odnośnie drugiej części polecenia −−−−> przełóżmy ten czworościan tak, aby ABD był podstawą 6. Zauważmy, że obie bryły powstałe po przecięciu przez przekrój to ostrosłupy o tej samej wysokości (wierzchołek w C), więc stosunek ich objętości = stosunkowi pól podstaw.

	1
7. Zauważmy, że pole podstawy trójkąta AEF będzie równe		PABC
	4

8. związku z tym stosunek objętości figur będzie wynosił .... 1 : 3