Potrzebuje pomocy z tym zadaniem. Fluu: 3. W trapezie prostokątnym opisanym na okręgu stosunek krótszej podstawy do promienia okręgu wpisanego wynosi 3:2. Pole trapezu wynosi 36. Oblicz pole kola wpisanego oraz odległości wierzchołków trapezu od jego dłuższej przekątnej.

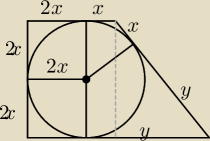
wredulus_pospolitus: z Tw. Pitagorasa: (y−x)² + (4x)² = (x+y)²

	4x*(5x+y)
ze wzoru na pole trapezu: 36 =
	2

stąd wyliczysz ile wynosi 2x

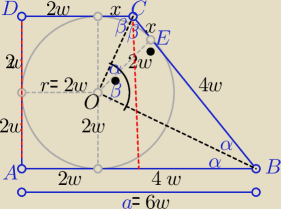
uuu: w prostokątnym ΔBOC (2w)²=4w*x ⇒ x= w

	6w+3w
P=		*4w=36 ⇒ w2=2 to w=√2
	2

P_k=... |DA|=|CF|=h=..........

Fluu: nie rozumiem czy mógłbyś wytłumaczyc ?

Fluu: a ok dzięki nie już wszystko wiem

Fluu: a czy w tym tw pit nie powinno byc samo y zamiast y−x?

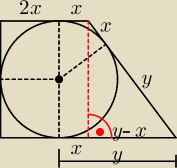
wredulus_pospolitus: nie, nie jest to 'sam y'

uuu: y=4x bez obliczania bo a= 2x+y=6x⇒ y=4x

wredulus_pospolitus: uuu −−− mimo wszystko 'jakieś obliczenia' są potrzebne czyli: 1. pokazanie że OEC podobny do BOE 2. zastosowanie proporcji Ale masz rację ... zauważenie tego mocno ułatwi sprawę ... tyle że nie wyjaśniłeś uczniowi skąd to się bierze i spodziewam się, że chłop nie ma pojęcia dlaczego tak jest.

wredulus_pospolitus: Oczywiście ... jeżeli będzie chociaż trochę dociekliwy to zrozumie ... tyle tylko ... czy jest 'trochę dociekliwy' czy też nie

uuu:

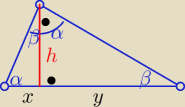
uuu: Warto to wiedzieć ( jest też ta zależność w karcie wzorów − w(trójkąt prostokątny)

h		y
	=		⇒ h2=x*y
x		h

dlatego w tym zad: (2w)²=4w*x ⇒ 4w²=4wx ⇒ w=x

. : @uuu bardziej mi chodziło o 'dociekliwosc' w tym dlaczego BOC jest prostokątny

uuu: Zaznaczyłam,że : 2α+2β=180^o ⇒ α+β=90^o ⇒ Δ BOC prostokątny

wredulus_pospolitus: Nie oto mi chodziło ... ale teraz to się przyczepię Kolejność w jakiej wykazujemy winna być: 1. .... to co Fiuu ma zauważyć ... więc nie będziemy mówić co to jest więc 2. ∡BOC = 90^o więc 3. ΔOEC podobny do ΔBEO podobny do ΔBOC Ty proponujesz wykazywanie: a. ΔOEC podobny do ΔBEO więc b. ∡BOC = 90^o a wtedy pojawia się pytanie ... skąd wiemy (bez wcześniejszego wykazania że ∡BOC = 90^o), że ΔOEC podobny do ΔBEO Oczywiście, to się sprowadza do 'magicznego' punktu 1. ... którego celowo nie podaje, aby Fiuu spróbował sam na to wpaść. Rozumiesz o co mi chodzi? Zakładasz (poprawnie ... ale nadal zakładasz) podobieństwo trójkątów bez wcześniejszego pokazania dlaczego taki wniosek możemy akurat w tym przypadku możemy wyciągnąć (a w wielu innych przypadkach nie będziemy mogli tego zrobić)

Fluu: ok bardzo dziękuje

uuu:

Fluu: czy ja musze przyjąć ze A jest (0,0)? żeby obliczyć odległoć tych wierzchołków?

Podstawy Geometrii: Trójkąt BOC jest trójkątem prostokątnym bo : . 1)Srodek (O) okręgu wpisanego w czworokąt leży na przecięciu sie dwusiecznych kątów 2)Dwusieczne kątów przyległych przecinają sie pod kątem prostym Kąty B i C sa to kąty przyległe stąd ∡COB jest kątem prostym ,więc ΔBOC jest trójkątem prostokątnym rysunek z godz 22 : 18

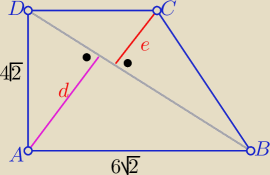
uuu: |BD|= 2√26

	d*|BD|
P(ABC)= 24 i P=		to d=...
	2

	e*|BD|
P(BCD)=36−24=12 to P=		to e=...
	2

uuu: poprawiam : P(ABD)=24

Fluu: dziękuje bardzo za pomoc <3