Równanie trygonometryczne maturzysta:

	1
Rozwiąż równanie 2*sin(2x) +		= 4*cos(x) w zbiorze [0, 2π].
	tg(x)

Bardziej chodzi mi o ilość rozwiązań, bo ten tangens wprowadza niejasność. Logika mówi co innego a kalkulator graficzny co innego.

Krzysiek:

1
	=ctgx
tgx

2*sin(2x)+ctg(x)=4cosx sin(x)≠0 ze względu na ctg(x)

	cos(x)
2*2sinx*cosx+		=4cos(x)
	sin(x)

4sin2(x)cos(x)+cos(x)
	=4cos(x)
sin(x)

4sin2(x)*cos(x)+cos(x)
	−4cos(x)=0
sin(x)

4sin2(x)cosx+cos(x)−4cosxsinx
	=0
sin(x)

To wyrazenie jest rowne o gdy licznik jest równy 0 4sin²x*cosx−4sinxcosx+cosx=0 cosx(4sin²x−4sin(x)+1)=0 cosx=0 lub 4sin²x−4sinx+1=0 (2sinx−1)²=0 2sinx−1=0 Potrafisz rozwiązac te dwa równania cosx=0 i 2sinx−1=0?

maturzysta: Tak, reszte potrafię rozwiązać ale właśnie mnie ten przypadek cos(x)=0 zastanawiał. Bo mamy tam

	1
		, więc wypadało by teoretycznie rozpatrzeć tg(x) ≠ 0. W końcu tak to było zapisane
	tg(x)

i żeby przekształcić tożsamościowo to w mianowniku nie może być 0.

	sin(x)
Wtedy		≠ 0, więc
	cos(x)

1) Licznik nie może zerować sin(x) ≠ 0 <=> x ≠ kπ, k∊ℤ 2) Mianownik różny od zera cos(x) ≠ 0 <=> x ≠ ^π₂ + kπ, k∊ℤ Co do rozwiązania D: x∊[0, 2π] 1) cos(x) = 0 <=> x = ^π₂ + kπ, k∊ℤ k = 0 => x = ^π₂∊D k = 1 => x = ^3π₂∊D Dalej nie sprawdzam bo poza dziedziną 2) 2sin(x) − 1 = 0 sin(x) = ¹₂ <=> x = ^π₆ + 2kπ ∨ x = ^5π₆ + 2kπ, k∊ℤ k = 0 => x = ^π₆∊D ∨ x = ^5π₆∊D Dalej tez poza dziedziną Zatem x∊{^π₆; ^π₂; ^3π₂; ^5π₆}

maturzysta:

	1
W szkole normalnie mnie uczono że		= ctg(x), ale ponieważ nie ma tego już w
	tg(x)

programie to i zadanie takie na około. No i przez to jest nieścisłość, bo niektórzy mówią że są 2 rozwiązania, a niektórzy że 4.

Krzysiek: A widzisz . Możesz miec racje w tym przypadku .

	1
Bo mianownik nie może sie zerowąc ze wzgledu na tangens czyli cosx≠0 a potem		nie
	tgx

może sie zerowac ze względu na ctg Więc rozwiązanie cosx=0 musimy odrzucic .

Krzysiek: Może wredulus spojrzy

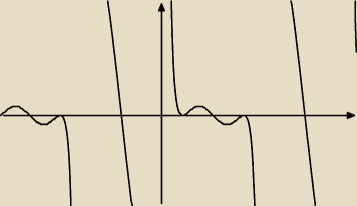
maturzysta: Jako tako udało mi się wykres tutaj załączyć

	1
y = 2*sin(2x) +		− 4*cos(x)
	tg(x)

No i właśnie na kalkulatorach graficznych wychodzą 4 rozwiązania. I nie wiem co z tym faktem zrobić xD Przed tamtą kreską w prawym górnym rogu dopiero x sięga 2π.

wredulus_pospolitus: nie ma żadnej nieścisłości: zał. cos ≠ 0 ∧ tgx ≠ 0 co powoduje, że część wyników należy odrzucić.

wredulus_pospolitus: Kalkulatory graficzne NIE biorą pod uwagę założeń wstępnych.

	x2
Wstukaj sobie f(x) =		narysuje Ci prostą y = x z Df = R
	x

https://www.wolframalpha.com/input?i=plot%5Bx%5E2%2Fx%5D

maturzysta: Okej, o tym nie pomyślałem. Czyli ostatecznie x∊{^π₆; ^5π₆}. Jak rozumiem to gdyby tam od razu był ctg(x), to nie bierzemy wtedy cos(x) ≠ 0 pod uwagę. Ale że mamy w takiej postaci, to musimy wyznaczyć dziedzinę wyjściowego równania i nam odpadnie wtedy ten cosinus.

wredulus_pospolitus: dokładnie

chichi: oczywiście, że biorą pod uwagę, gdy go zapytasz ile wynosi f(0) to wypluje niezdefiniowane, tam jest dziura w jednym argumencie, ale tego nie widać, my zwykliśmy w układzie robić wielkie otwarte kropy, do których wpada... spoooooooro argumentów

chichi: https://www.desmos.com/calculator/ifchuxjylm