Wysokość w trójkącie prostokątnym z wierzchołka kąta prostego xyz: Proszę o pomoc z tym zadaniem W trójkącie prostokątnym z wierzchołków kąta prostego poprowadzono wysokość o długości 2. Oblicz długości docinków na jakie dzieli ta wysokość przeciwprostokątną o długosci 5. Jakie jest tu rozwiązanie najprostszym możliwym sposobem?

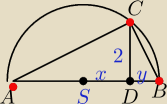
Krzysiek: Rysujemy odcinek AB równy przeciwprostokatnej Ze srodka odcinka AB kresllimy półokrag promieniem AS Kreslimy wysokośc CD równa 2 trójkat ABC bedzie trójkatem prostokatnym bo kąt wpisany ACB oparty na srednicy ma 90^o Mierzymy odcinek x i odcinek y mamy tez w trójkącie prostokatnym h=√x*y h²=x*y 4=4*1 x=4 i y=1

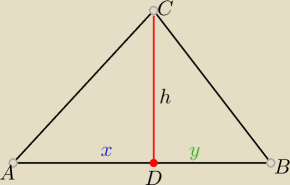
Jolanta: Wysokość dzieli przeciwprostokątna na dwa odcinki. x. i. y I jest taka zależność h²=x*y Bierze się to z podobieństwa trojkatow Narysuj trójkąt prostokątny np 3 kratki w pionie w prawo 9 kratek to nasze przyprostokątne,poprowadź wysokość z kąta prostego Mamy dwa trójkąty podobne h jest ich wspólnym bokiem Na przeciwprostokątnej krótki odcinek zaznaczę x a dłuższy y

h		y
	=
x		h

Mnożymy na ukos i mamy h²=x*y x+y=5. y = 5−x 2²=x*(5−x). Jasne? ,

Krzysiek:

Jolanta: 4=5x−x² x²−5x+4=0 Δ=b²−4ac=25−16=9√Δ=3 x>0 i x<5

	−b−√Δ		5−3
x1=		=		=1. y=5−1=4
	2a		2

	5+3
x2=		=4. y=5−4=1
	2

Czyli przeciwprostokątnej na podzielona jest na dwa odcinki o długości 1 i 4

Xyz: Dzięki wam za pomoc