prawdopodobienstwo
matematycznyswir: Kazde z dziewieciu krzesel malujemy na jeden z trzech kolorow. Kolor kazdego krzesla
wybieramy losowo. Oblicz prawdopodobienstwo zdarzenia polegajacego na tym, ze wsrod
tych 9 krzesel przynajmniej 4 beda pomalowane tym samym kolorem, jesli wiadomo, ze do
pomalowania krzesel kazdy z kolorów został zuzyty przynajmniej raz.
Prosze o pomoc bo trace glowe.
15 mar 22:24
wredulus_pospolitus:
wiemy, że każdy kolor został wybrany co najmniej raz

mamy policzyć szansę na to, że chociaż jeden z kolorów został użyty minimum 4 razy.
zauważ, że zatem JEDYNA (rozkład) sytuacja kiedy to nie zajdzie to gdy będziemy mieli 3 krzesła
każdego koloru

Wiedząc to liczymy z prawdopodobieństwa przeciwnego.
Dla ułatwienia ustalamy, że krzesła są ponumerowane:
dlaczego taka |Ω|

Otóż:
1. 3
9 −−− każde krzesło wybiera sobie jeden z trzech kolorów ... ale to umożliwia nam sytuację
w których wykorzystaliśmy mniej niż 3 kolory
2. 3*2
9 −−− sytuacje gdzie 'odrzuciliśmy jeden kolor' i krzesła wybierają sobie jeden z dwóch
kolorów ... i to także umożliwia nam sytuację w których wykorzystaliśmy dokładnie 1 kolor
3. zauważ, że w 3*2
9 policzyliśmy PODWÓJNIE sytuacje gdzie wszystkie krzesła są pomalowane na
jeden kolor (tj. odrzucamy czerwony, z niebieskiego i zielonego wszystkie krzesła wybrały
zielony .... druga sytuacja: odrzucamy niebieski, z czerwonego i zielonego wszystkie krzesła
wybrały zielony)
4. dlatego musimy dodać 3 (podwójnie zliczone) przypadki
Natomiast |A| to po prostu wybranie po 3 krzesła dla każdego z kolorów.
Więc ostatecznie:
Mam nadzieję, że wytłumaczyłem dlaczego te wartości
15 mar 22:55
matematycznyswir: dziękuję

mógłbyś jeszcze pomóc mi z tym?
środkowa AD trójkąta ABC przecina okrąg wpisany w ten trójkąt w punktach K i L, przy czym
|AK|<|AL|. wykaż, że jeśli |AK|=|DL| to |BC|=2|AC|
15 mar 23:08
wredulus_pospolitus:
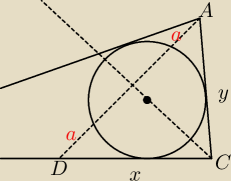
Ugh ... planimetria − moja pięta Achillesowa

1. prowadzimy dwusieczną z wierzchołka C (będzie ona przechodzić przez środek okręgu −> patrz
związek pomiędzy przecięciem dwusiecznych a środkiem okręgu wpisanego w trójkąt)
2. jeżeli wykażemy, że jest ona prostopadła do środkowej ... to będziemy mieli równość x = y
(trójkąty ADC jest równoramienny)
A jak to wykazać ... szczerze mówiąc, nie wiem ... jakoś trzeba skorzystać z faktu, że mamy
tutaj środkową.
16 mar 01:00
aa:
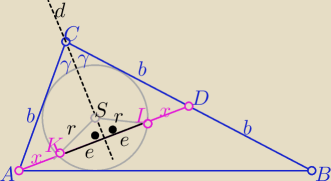
ΔKSL równoramienny( o ramionach
r
więc
dwusieczna
d prostopadła do środkowej AD
zatem ΔADC też równoramienny
co kończy dowód
|BC|=2|AC|
16 mar 09:59
. :
Wow wow wow... na jakiej podstawie dwusieczna d jest dwusieczna S bądź prostopadła do środkowej
AD?
Napisanie że tak jest to nie wykazanie tego.
16 mar 12:49
aa:
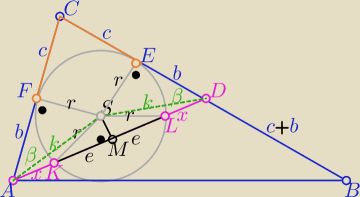 wreduśny
wreduśny
A teraz? pasuje?
ΔAFS≡ΔDSE z cechy (bkb) to |AF|=|DE|=b
i dwusieczna CS pokrywa się z CM i jest prostopadła do środkowej AD

16 mar 17:39
wredulus_pospolitus:
Oooookeeeeyyy ... ale nadal się przyczepię

(no muuuuszę

inaczej nie będę sobą

):
0. na podstawie ∡AFS = ∡DES , |FS| = |ES| , |AS| = |SD| NIE MASZ jeszcze cechy bkb (bo na ten
moment masz kbb) ... ale po dołożeniu tw. Pitagorasa już masz to co chcesz, czyli |AF|=|DE|,
ale i także bkb)
1. nadal nie pokazałeś dlaczego CS pokrywa się z CM (oczywiście ... to wynika z tego rysunku,
ale to wykazujesz z tego że ΔADC jest równoramienny ... a nie, że ΔADC jest równoramienny bo
CM jest dwusieczną kąta w wierzchołku C).
2. w efekcie wykazujesz w ten sposób: ΔADC jest równoramienny, więc CM jest dwusieczną i
prostopadła do AD, więc ΔADC jest równoramienny

3. tak naprawdę równoramienność ΔADC wykazujesz wcześniej, bez korzystania z tego że CM jest
dwusieczną (a korzystając tylko z tego że CS jest dwusieczną oraz z |AF|=|DE|=b)
Ale jak najbardziej −−− jest to wykazanie tego co trza było wykazać

I zdaję sobie sprawę z tego, że skrótowo zapisujesz ... ale w akurat w geometrii to chyba nie
jest za dobry pomysł

16 mar 18:22
aa:
to jeszcze tak ( chyba najprostszy sposób)
1 / |CF|=|CE|=c z tw. o odcinkach stycznych
2/ z tw. o stycznej i siecznej
raz z jednej strony tak:
|AF|2= |AK|*|AL|
i z drugiej strony :
|DE|2= |DL|*|DK|
i z tego mamy |AF|2=|DE|2
|AF|=|DE|= b
...........
i teza
16 mar 18:40
Mila:
9:59

16 mar 22:29
Julia A. McCall: Interesting probability problem! It feels like navigating a tricky slope in Snow Rider, doesn't
it? We need to consider the constraint that each color is used at least once when calculating
the probability of having at least four chairs sharing the same color. Seems like a complex
level in the game, requiring careful planning and execution. Good luck finding the solution!
https://snowridergame.io
24 kwi 05:28
jory: To solve the probability problem, it's important to calculate the complementary probability
first, which helps in understanding the chances of having at least 4 chairs of the same color.
As for the geometry problem, the key idea is recognizing the properties of the triangle and
applying the fact that the median and angle bisector are related, ultimately leading to the
desired equality.
https://www.ailogogenerator.sh/
2 lip 08:49
 mamy policzyć szansę na to, że chociaż jeden z kolorów został użyty minimum 4 razy.
zauważ, że zatem JEDYNA (rozkład) sytuacja kiedy to nie zajdzie to gdy będziemy mieli 3 krzesła
każdego koloru
mamy policzyć szansę na to, że chociaż jeden z kolorów został użyty minimum 4 razy.
zauważ, że zatem JEDYNA (rozkład) sytuacja kiedy to nie zajdzie to gdy będziemy mieli 3 krzesła
każdego koloru  Wiedząc to liczymy z prawdopodobieństwa przeciwnego.
Dla ułatwienia ustalamy, że krzesła są ponumerowane:
Wiedząc to liczymy z prawdopodobieństwa przeciwnego.
Dla ułatwienia ustalamy, że krzesła są ponumerowane:
 Otóż:
1. 39 −−− każde krzesło wybiera sobie jeden z trzech kolorów ... ale to umożliwia nam sytuację
w których wykorzystaliśmy mniej niż 3 kolory
2. 3*29 −−− sytuacje gdzie 'odrzuciliśmy jeden kolor' i krzesła wybierają sobie jeden z dwóch
kolorów ... i to także umożliwia nam sytuację w których wykorzystaliśmy dokładnie 1 kolor
3. zauważ, że w 3*29 policzyliśmy PODWÓJNIE sytuacje gdzie wszystkie krzesła są pomalowane na
jeden kolor (tj. odrzucamy czerwony, z niebieskiego i zielonego wszystkie krzesła wybrały
zielony .... druga sytuacja: odrzucamy niebieski, z czerwonego i zielonego wszystkie krzesła
wybrały zielony)
4. dlatego musimy dodać 3 (podwójnie zliczone) przypadki
Natomiast |A| to po prostu wybranie po 3 krzesła dla każdego z kolorów.
Więc ostatecznie:
Otóż:
1. 39 −−− każde krzesło wybiera sobie jeden z trzech kolorów ... ale to umożliwia nam sytuację
w których wykorzystaliśmy mniej niż 3 kolory
2. 3*29 −−− sytuacje gdzie 'odrzuciliśmy jeden kolor' i krzesła wybierają sobie jeden z dwóch
kolorów ... i to także umożliwia nam sytuację w których wykorzystaliśmy dokładnie 1 kolor
3. zauważ, że w 3*29 policzyliśmy PODWÓJNIE sytuacje gdzie wszystkie krzesła są pomalowane na
jeden kolor (tj. odrzucamy czerwony, z niebieskiego i zielonego wszystkie krzesła wybrały
zielony .... druga sytuacja: odrzucamy niebieski, z czerwonego i zielonego wszystkie krzesła
wybrały zielony)
4. dlatego musimy dodać 3 (podwójnie zliczone) przypadki
Natomiast |A| to po prostu wybranie po 3 krzesła dla każdego z kolorów.
Więc ostatecznie:
 mógłbyś jeszcze pomóc mi z tym?
środkowa AD trójkąta ABC przecina okrąg wpisany w ten trójkąt w punktach K i L, przy czym
|AK|<|AL|. wykaż, że jeśli |AK|=|DL| to |BC|=2|AC|
mógłbyś jeszcze pomóc mi z tym?
środkowa AD trójkąta ABC przecina okrąg wpisany w ten trójkąt w punktach K i L, przy czym
|AK|<|AL|. wykaż, że jeśli |AK|=|DL| to |BC|=2|AC|
 Ugh ... planimetria − moja pięta Achillesowa
Ugh ... planimetria − moja pięta Achillesowa  1. prowadzimy dwusieczną z wierzchołka C (będzie ona przechodzić przez środek okręgu −> patrz
związek pomiędzy przecięciem dwusiecznych a środkiem okręgu wpisanego w trójkąt)
2. jeżeli wykażemy, że jest ona prostopadła do środkowej ... to będziemy mieli równość x = y
(trójkąty ADC jest równoramienny)
A jak to wykazać ... szczerze mówiąc, nie wiem ... jakoś trzeba skorzystać z faktu, że mamy
tutaj środkową.
1. prowadzimy dwusieczną z wierzchołka C (będzie ona przechodzić przez środek okręgu −> patrz
związek pomiędzy przecięciem dwusiecznych a środkiem okręgu wpisanego w trójkąt)
2. jeżeli wykażemy, że jest ona prostopadła do środkowej ... to będziemy mieli równość x = y
(trójkąty ADC jest równoramienny)
A jak to wykazać ... szczerze mówiąc, nie wiem ... jakoś trzeba skorzystać z faktu, że mamy
tutaj środkową.
 ΔKSL równoramienny( o ramionach r
więc
dwusieczna d prostopadła do środkowej AD
zatem ΔADC też równoramienny
co kończy dowód
|BC|=2|AC|
ΔKSL równoramienny( o ramionach r
więc
dwusieczna d prostopadła do środkowej AD
zatem ΔADC też równoramienny
co kończy dowód
|BC|=2|AC|
 wreduśny
A teraz? pasuje?
ΔAFS≡ΔDSE z cechy (bkb) to |AF|=|DE|=b
i dwusieczna CS pokrywa się z CM i jest prostopadła do środkowej AD
wreduśny
A teraz? pasuje?
ΔAFS≡ΔDSE z cechy (bkb) to |AF|=|DE|=b
i dwusieczna CS pokrywa się z CM i jest prostopadła do środkowej AD

 (no muuuuszę
(no muuuuszę  inaczej nie będę sobą
inaczej nie będę sobą  ):
0. na podstawie ∡AFS = ∡DES , |FS| = |ES| , |AS| = |SD| NIE MASZ jeszcze cechy bkb (bo na ten
moment masz kbb) ... ale po dołożeniu tw. Pitagorasa już masz to co chcesz, czyli |AF|=|DE|,
ale i także bkb)
1. nadal nie pokazałeś dlaczego CS pokrywa się z CM (oczywiście ... to wynika z tego rysunku,
ale to wykazujesz z tego że ΔADC jest równoramienny ... a nie, że ΔADC jest równoramienny bo
CM jest dwusieczną kąta w wierzchołku C).
2. w efekcie wykazujesz w ten sposób: ΔADC jest równoramienny, więc CM jest dwusieczną i
prostopadła do AD, więc ΔADC jest równoramienny
):
0. na podstawie ∡AFS = ∡DES , |FS| = |ES| , |AS| = |SD| NIE MASZ jeszcze cechy bkb (bo na ten
moment masz kbb) ... ale po dołożeniu tw. Pitagorasa już masz to co chcesz, czyli |AF|=|DE|,
ale i także bkb)
1. nadal nie pokazałeś dlaczego CS pokrywa się z CM (oczywiście ... to wynika z tego rysunku,
ale to wykazujesz z tego że ΔADC jest równoramienny ... a nie, że ΔADC jest równoramienny bo
CM jest dwusieczną kąta w wierzchołku C).
2. w efekcie wykazujesz w ten sposób: ΔADC jest równoramienny, więc CM jest dwusieczną i
prostopadła do AD, więc ΔADC jest równoramienny  3. tak naprawdę równoramienność ΔADC wykazujesz wcześniej, bez korzystania z tego że CM jest
dwusieczną (a korzystając tylko z tego że CS jest dwusieczną oraz z |AF|=|DE|=b)
Ale jak najbardziej −−− jest to wykazanie tego co trza było wykazać
3. tak naprawdę równoramienność ΔADC wykazujesz wcześniej, bez korzystania z tego że CM jest
dwusieczną (a korzystając tylko z tego że CS jest dwusieczną oraz z |AF|=|DE|=b)
Ale jak najbardziej −−− jest to wykazanie tego co trza było wykazać  I zdaję sobie sprawę z tego, że skrótowo zapisujesz ... ale w akurat w geometrii to chyba nie
jest za dobry pomysł
I zdaję sobie sprawę z tego, że skrótowo zapisujesz ... ale w akurat w geometrii to chyba nie
jest za dobry pomysł 
