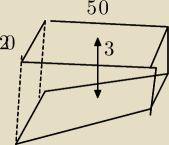
Długość basenu pływackiego jest równa 50m, a jego szerokość wynosi 20m. Głębokoś Carollo: Długość basenu pływackiego jest równa 50m, a jego szerokość wynosi 20m. Głębokość basenu na jego środku jest równa 3m. a) oblicz objętość basenu b) oblicz łączną powierzchnie wszystkich ścian bocznych basenu. Widziałem tylko, że można zastosować zależność, że a+b/2=3, ale obliczylem 4 bryły i dalej mam objetosc ze zmienna a. nie wiem co dalej. Prosze o pomoc. Będę wdzięczny ;}

M: https://matematykaszkolna.pl/forum/374009.html

Carollo: To już widziałem, mówię. Nadal nie rozumiem co dalej

Carollo: Znam tą zależność w trapezie równoramiennym, ba nawet sam do tego doszedłem. Tylko potrzebuję wiedzieć co dalej bo mam objetosc policzoną z a bo b=6−a i sobie podstawiłem i dalej nie wiem co

Carollo: Z resztą na forum co wysłałeś też nie ma tego opisanego

wredulus_pospolitus: 1. Zauważ, że w przekroju ten basen jest trapezem. V_basenu = P_trapezu*H_{czyli szerokość basenu} =

	(a+b)
=		*h*H = 3*50*20
	2

natomiast odnośnie powierzchni bocznej, zauważ:

	a+b		a+b
Pb = 20b + 2*		*50 + 20a = 20(a+b) + 50(a+b) = 70(a+b) = 140		=
	2		2

wredulus_pospolitus: Jak widzisz ... bez względu jak 'wielki skos' (różnica głębokości) będzie w basenie ... jego powierzchnia boczna oraz objętość będzie taka sama (o ile średnia głębokość jest stała)

wredulus_pospolitus: Czy wiesz 'dlaczego' tak jest

Carollo: Faktycznie, teraz, zauważyłem. Dziękuję za wyjaśnienie

Carollo: Jest to trapez równoramienny, więc bezwzględu na dlugosc skosu, powierzchnia boczna bedzie taka sama. Jezeli chodzi o objetosc to też, o ile faktycznie srodkowa dlugosc − srednia w tym przypadku, bedzie taka sama.

Carollo: w sensie nie równoramienny, ale wiem o co chodzi − wysokość się nie zmieni