Planimetria Kamilox: oblicz pole trojkata rownoramiennego wpisanego w okrag o promieniu R, jesli podstawa trojkata ma dlugosc R

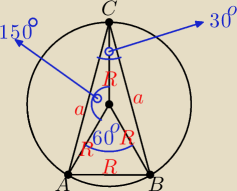
Mei Lin: |AB|=R |OA|=|OB|=R |CO|=R trójkat AOB jest trójkatem równobocznym o boku równym R |OD|=h₁ wysokośc w trójkacie równobocznym AOB

	R√3
h1=
	2

Wysokośc (h) trójkata równoramiennego ABC h=R+h₁

	R√3		2R+R√3		R(2+√3)
h=R+		=		=		)
	2		2		2

	R		R(2+√3)		R2(2+√3
P=		*		=
	2		2		4

Olek: Proponuję bez obliczania wysokości

Kamilox: Dziękuję

Olek:

	1
sin150o = sin30o =
	2

	1		1
Pole trójkąta ABC: P =		R2*sin30o*2 +		R2√3 = ...
	2		4