stereometria sześcian kas: Sześcian o krawędzi długości a przecięto płaszczyzną, przechodzącą przez przekątną podstawy i nachyloną do płaszczyzny podstawy pod kątem o mierze 60 stopni. Otrzymano pewien przekrój. Oblicz promień okręgu opisanego na tym przekroju. wiem, że przekrój będzie trapezem równoramiennym, wyznaczyłam długości jego podstaw i wysokość w zależności od a, ale nie wiem co dalej zrobić

wredulus_pospolitus: Chyba najszybciej będzie: 1. obliczamy przekątna trapezu. 2. przekątna podzieliła nam trapez na dwa trójkąty, bierzemy jeden z nich i wstawiamy do wzoru:

	abc
R =
	4P

wredulus_pospolitus: alternatywnie ... możemy utworzyć układ równań dla dwóch trójkątów (bo pola trójkątów już możesz policzyć) i wtedy długość przekątnej i promień wyliczymy po prostu z tego układu. Tak chyba będzie jeszcze szybciej (i prościej).

Iryt: Podaj te obliczone wartości:

Iryt: To komentarz dla kas.

kas: wiadomo, że dolna dłuższa podstawa to będzie przękatna podstawy sześcianu czyli a√2, h będzie 2√3a/2 a górna podstawa to a√2 −2/3 a√3.

kas: probowalam obliczyć to taki sposób jak wredulus_pospolitys proponował, ale wynik wychodził tak kosmiczny, że nie wiem czy gdzieś nie mam blędu

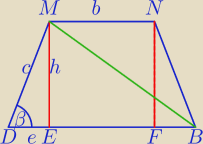
Mila: Dobrze, zgadza się , ale w tej chwili mam "kosmiczny" katar, będę liczyć wieczorem. Podpowiedź:

	DB+MN
|EB|=
	2

e=a√2−|EB| To już Ci pomoże w obliczeniach w ΔDEM. Do wieczora

Mila: No i co ? Obliczyłaś R. Ja mam obliczone, ale jestem w kiepskiej formie, to wynik może być (?). Napisz Twój wynik. Obliczenia nie są jakieś obłędne.

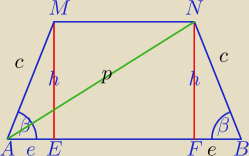
Mila: 1)

	2a√3		2
|AB|=a√2, h=		, |MN|=a√2−		a√3
	3		3

2)

|AB|+|MN|		a√3
	=a√2 −		=|AF|
2		3

	a√3		a√3		a√5
|EB|=a√2 −		, |AE|=|FB|=		, c=
	3		3		√3

3)

	1		2
W ΔBFN: cosβ=		, sinβ=
	√5		√5

w ΔABN: p²=|AB|²+c²−2*c*|AB|cosβ albo

	a√3		2a√3
W ΔAFN: p2=(a√2 −		)2+(		)2
	3		3

	a2
p2=		*(11−2√6)
	3

	p
4)		=2R
	sinβ