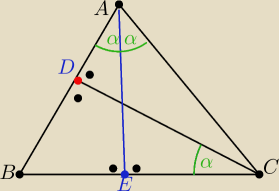
Ramiona parami prostopadłe Podstawy Geometrii: Było takie zadanie W trójkącie równoramiennym ABC kąt A jest katem przy wierzchołku trójkąta Z wierzchołka C wykreślono wysokość CD względem boku AB . Udowodnić że kąt A jest dwa razy większy od kąta BCD Jest wskazówka Wykreślcie dwusieczna kąta A i skorzystajcie z twierdzenia o kątach mających parami wzajemnie prostopadłe ∡BCD=α jest równy ∡BAE BC⊥AE CD⊥AB Katy te mają ramiona parami prostopadłe więc kąty te sa równe W związku z tym że AE jest dwusieczna kąta A to kąt A jest dwa razy większy od kąta BCD. A jeśli nie byłoby tej wskazówki to jak to zrobić?

723: A które boki w tym trójkącie są równe?

Mei Lin: AB =AC

723: Skorzystaj z podobieństwa trójkątów (prostokątnych)

Mei Lin: OK Chociaż podobieństwo będzie póżniej