|AB | = 30 , |BC | = |AC | = 3 9 Carollo: Podstawą ostrosłupa ABCS jest trójkąt równoramienny ABC , w którym |AB | = 30 , |BC | = |AC | = 3 9 i spodek wysokości ostrosłupa należy do jego podstawy. Każda wysokość ściany bocznej poprowadzona z wierzchołka S ma długość 26. Oblicz objętość tego ostrosłupa. r=promien wpisanego okregu w trojkat R=promien opisanego okregu na trojkacie Czy mogę skorzystać ze wzoru abc/4R skoro spodek wysokosci ostroslupa dzieli wysokosc podstawy trojkata rownoramiennego na r i R? Widzialem rozwiazanie z r ale przeciez z R tez to mozna zrobic a mi nie wychodzi tym sposobem Prosze o wytlumaczenie

chichi: "Czy mogę skorzystać ze wzoru abc/4R skoro spodek wysokosci ostroslupa dzieli wysokosc podstawy trojkata rownoramiennego na r i R?" skąd płynie ten wniosek? przecież środki okręgów wpisanego i opisanego na trójkącie nie pokrywają się, gdy trójkąt ten nie jest równoboczny...

Carollo: Ten wniosek płynie z tego, że wysokość trójkąta równoramiennego jest zarówno symetralną i dwusieczną. Aaaa... już zrozumiałem to że jest to symetralna i dwusieczna to jest to racja ale dwusieczne kątów w tym trojkącie przecinają się gdzie indziej niz w przypadku symetralnych. Wniosek: Leżą na tej samej wysokosci trojkata równoramiennego ale srodki okregow znajduja sie gdzie indziej na tej wysokosci

chichi: Nie koniecznie... środek okręgu opisanego na trójkącie równoramiennym, który jest rozwartokątny leży na przedłużeniu wysokości

Carollo: No tak, leży na przedłużeniu a w ostrokatnym lez juz na wysokosci wewnatrz

klen22: nie wiem

Jolanta: Masz promień okręgu wpisanego?

Jolanta: Masz promień okręgu wpisanego?

Podstawy Geometrii: Jesli spodek wysokości ostrosłupa nalezy do podstawy to oznacza że wysokośc ta będzie prostopadła do podstawy

	P
r=
	p

	2*39+30		108
p=		=		=54
	2		2

P=√p(p−a)(p−b)(p−b) P=√54*24*15*15=540

	540
r=		=10
	54

chichi: a czy wysokość może nie być prostopadła? przecież tak jest zdefiniowana...

Podstawy Geometrii: Bardziej chodziło mi o to że nie bedzie padac wewnątrz trójkata czy na zewnątrz

Jolanta: Środek okręgu jest spadkiem wysokości ostrosłupa jeżeli wszystkie ściany nachylone są pod tym samym kątem do podstawy

Jolanta: Środek okręgu jest spadkiem wysokości ostrosłupa jeżeli wszystkie ściany nachylone są pod tym samym kątem do podstawy

Podstawy Geometrii: Mozna prosić o rozwiązanie z tym promieniem r .

Jolanta: r²+H²=26²

Jolanta: 10²+H²=676 H=√576=24

	1
V=		Pp*H
	3

Wysokość trójkąta w podstawie z tw Pitagorasa

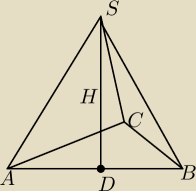
Podstawy Geometrii: Jolanta Moze ja czegoś nie rozumiem Nie bardzo rozumiem do czego ten promien jest potrzebny Spodek (D) wysokości (H) leży na podstawie

Jolanta: 15²+h²=39² h=√2521−225=36

	30*36
Pp=		=540
	2

	1
V=		*540*24=4320
	3

Jolanta: No tak nie doczytałam Jakoś głupio zasugerowałem się jak pytał o promień okregu

Podstawy Geometrii: Dziękuję

Jolanta: Za co?

Jolanta: Za co?

Podstawy Geometrii: Z grzeczności

Karola:

Jolanta: A moz wiesz dlaczego wysyła mi się podwójnie skoro tylko raz naciskam ?

Jolanta: A moz wiesz dlaczego wysyła mi się podwójnie skoro tylko raz naciskam ?

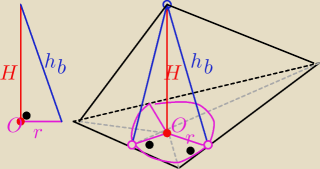
Mila: SO⊥pł. ABC to z tw_3⊥ jest prostopadła każdej prostej tej pł. przechodzącej przez punkt przebicia O. ΔSOD≡ΔSOE≡ΔSOF ( cecha ? )⇒OD=OE=OF O jest środkiem okręgu wpisanego w ΔABC Dalej potrafisz skończyć?

Podstawy Geometrii: Kiedyś mi także z komputera tak wysyłało . Po dwóch tygodniach sie skonczyło . Potrafie to dokończyc Mila Tylko jedno mnie zastanawia . czy to zadanie jest dobrze przepisane Spodek wysokości ostrosłupa to nie jest punkt O tylko punkt D (on pisze że należy do podstawy

Jolanta: Podstawy geometrii H nie może być na boku trójkąta

Jolanta: Chociaż w sumie dlaczego by nie

Jolanta: A nie jest tak,że ten ostrosłup jest pochyly Czyli liczymy z tw. Pitagorasa h postawy ,pole i podstawiamydo wzoru na V P_p=540 i H=26