proszę o rozwiązanie Ania: w trójkącie równoramiennym ABC podstawa AB ma długości 16 cm a ramiona BC i AC − 10cm sprawdź czy trójkąt jest ostrokątny czy rozwartokątny oblicz promień okręgu opisanego na tym trójkącie na dwa sposoby 10² + 10² = 8² 200 .< 256 ⇒ Δ ABC jest rozwartokątny CD = h = 6 cm z ΔB0C − prostokątny 8² + (R − 6 )² = R² ⇒ R = ²⁵₃ nie wiem jak obliczyć promień okręgu opisanego na tym trójkącie na dwa sposoby

.: Na przykład: Skorzystaj z Tw. Sinusow wykorzystując sinusa kąta ostrego.

Ania: ale nie braliśmy Tw. sinusów

Qbuś: W karcie wzorów masz:

	abc		abc
P=		⇒ R=
	4R		4P

i otrzymujesz

	25
R=
	3

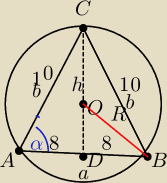
Podstawy Geometrii: h²=10²−8² h²=36 h=6

	h		6		3
sinα=		=		=
	10		10		5

	10
R=
	2sinα

Policz . Lub

	a*b*b
R=
	4P

Długości boków masz dane Pole trójkata tez policzysz .

Jolanta:

	abc
R=		Aniu a taki wzór ?
	4P

Jolanta: a ,b,c długości boków trójkąta P pole trójkąta Liczysz wysokość z tw Pitagorasa,pole trójkąta,promień okręgu

Ania: ale trójkąt jest rozwartokątny i środek okręgu nie należy do trójkąta leży poza trójkątem

Podstawy Geometrii: Rysunek do zadania jest poglądowy . Możesz sobie sama zrobic rysunek dokładny w zeszycie . natomiast wzory do obliczenia długości promienia okregu opisanego na trójkącie pozostana takie same

Ania: jeżeli obliczę R według wzoru R = ^abc_4P to promień okręgu nie jest równe R = ²⁵₃ które wcześniej obliczyłam a wynik w podręczniku jest to R = ²⁵₃

Ania: przepraszam za moje błędy wszystko jest dobrze i dziękuję bardzo za rozwiązanie

Jolanta:

Podstawy Geometrii: Ja także się uczę

Ania: a jak to obliczyć z podobieństwa odpowiednich trójkątów prostokątnych bo w poleceniu powyższy zadaniu jest jest aby skorzystać z podobieństwa odpowiednich trójkątów prostokątnych

wredulus_pospolitus: ale żeby co policzyć

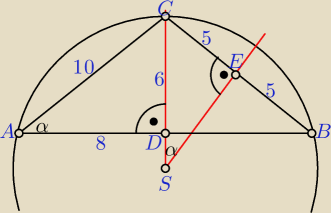
qstosz: Korzystamy z podobieństwa trójkątów. Promień R = |CS| = |ES|, środek okręgu opisanego jest punktem przecięcia symetralnych boków. ΔSED~ΔADC (kąt, kąt)

|CS|		|AC|		R		10		50		25
	=		⇒		=		⇒ R=		=
|CE|		|CD|		5		6		6		3

Ania: dziękuję bardzo

qstosz: mała poprawka: ΔSEC~ΔADC

Ania: dziękuję