trójkąt równoramienny Podstawy Geometrii: Udowodnic że ramie trójkąta równoramiennego jest większe od połowy podstawy

Jolanta: Niestety mam problem z dowodami Niby wszystko jasne ale jak to poprawnie zapisać? W trójkącie równoramiennym wysokość dzieli kat przy wierzchołku i podstawę na dwie równe czesci Powstają dwa trójkąty prostokątne ,w których wysokość i połowa podstawy są przyprostokątnymi a ramię trójkąta równoramiennego jest przeciwprostokatna Poniewaz w trójkącie naprzeciwko największego kąta leży najdłuższy bok , ramię trójkąta równoramiennego jest większe od połowy podstawy

Podstawy Geometrii: Dziękuję Ja także mam problem z dowodami .

Jolanta: Miałam nadzieję,że ktos skomentuje

wredulus_pospolitus: 1. prowadzimy wysokość 2. zauważamy, że wysokość dzieli trójkąt na dwa trójkąty przystające (cecha KBB). 3. stąd wiemy, że wysokość dzieli podstawę w połowie. 4. tw. Pitagorasa wieńczy dzieło.

chichi: e tam, pitagoras. w dowolnym trójkącie prostokątnym zachodzi: długość przeciwprostokątnej > długość przyprostokątnej

chichi:

	b
albo wprost z nierówności trójkąta a + a > b ⇔ a >
	2

Podstawy Geometrii: Ja to rozumiem

Jolanta: Ja też rozumiem ale nie wiem jak to powinno być prawidlowo napisane 0 samo pisanie chodzi

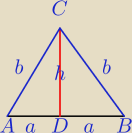
Iryt: |AB|=2a 2b>2a b>a

Jolanta: : )) Coraz więcej dowodow a ja raczej uczyłam się działań nie dowodzenia. Bratanica jest w drugiej klasie Dzielenia wielomianów nie mieli ale jakieś dowody o rusz

Joanna : Dowody były zawsze i zawsze było ich mniej niż innych zadań. Może dlatego Pani nie pamięta. Dzielenie wielomianów zostało usunięte z podstawy programowej na poziomie podstawowym