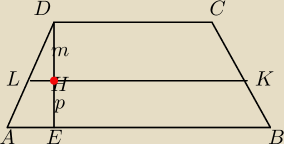
 Przez punkt H dzielący wysokość DE trapezu ABCD w stosunku m/p poprowadzono prostą równoległa
do podstawy AB która przecina boki BC i AD w punktach K i L. Wykaż, że KL = (ma+pb):(m+p)
Przez punkt H dzielący wysokość DE trapezu ABCD w stosunku m/p poprowadzono prostą równoległa
do podstawy AB która przecina boki BC i AD w punktach K i L. Wykaż, że KL = (ma+pb):(m+p)
| m | ||
3. stąd mamy: |LH| = |AE|* | (analogicznie z drugą wysokością) | |
| m+p |
| m | m | |||
4. zatem: |LK| = |CD|+ |AE|* | + |FB|* | = //// a = |AE| + |FB| + b //// | ||
| m+p | m+p |
| m | m | am | b(m + p) − bm | |||||
= b + a* | − b* | = | + | = | ||||
| m+p | m+p | m+p | m+p |
| am + bp | ||
= | gdzie a = |AB| ; b = |CD| | |
| m+p |
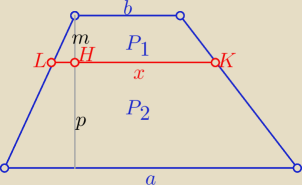 Można też tak:
Można też tak:
| a+b | ||
P(trapezu)= | *(m+p) | |
| 2 |
| x+b | x+a | |||
P1= | *m i P2= | *p | ||
| 2 | 2 |
| am+bp | ||
x= | ||
| m+p |