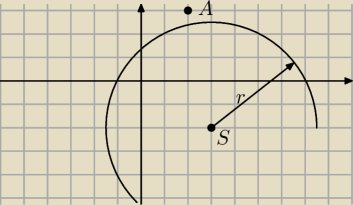
 1) dobrze jest sobie zrobic rysunek −widac wtedy gdzie lezy punkt A
U nas leży na zewnątrz okręgu więc będa dwie styczne (bedziemy szukac równan dwóch stycznych
2) ogólnie mamy że prosta przechodząca przez dany punkt ma równanie
y−y0=m(x−x0) (x0,y0) to wspólr5zedne punktu A u nas
Prosta przechodząca przez punkt A =(2,3) bedzie miała równanie
y−3=m(x−2)
================
3) Obliczamy odległość środka okręgu S=(3,−2) od prostej y−3=m(x−2)
a)Piszemy równanie tej prostej w postaci ogólnej
y−3=mx−2m
−mx+−2m+y−3=0
y−mx+2m−3=0 (robimy tak żeby to (mx) było dodatnie
mx−y−2m+3=0 (mamy już masz równanie tej prostej w postaci ogólnej
===============
b) Stosujemy wzór na odległośc punktu od prostej
Znamy ten wzór
1) dobrze jest sobie zrobic rysunek −widac wtedy gdzie lezy punkt A
U nas leży na zewnątrz okręgu więc będa dwie styczne (bedziemy szukac równan dwóch stycznych
2) ogólnie mamy że prosta przechodząca przez dany punkt ma równanie
y−y0=m(x−x0) (x0,y0) to wspólr5zedne punktu A u nas
Prosta przechodząca przez punkt A =(2,3) bedzie miała równanie
y−3=m(x−2)
================
3) Obliczamy odległość środka okręgu S=(3,−2) od prostej y−3=m(x−2)
a)Piszemy równanie tej prostej w postaci ogólnej
y−3=mx−2m
−mx+−2m+y−3=0
y−mx+2m−3=0 (robimy tak żeby to (mx) było dodatnie
mx−y−2m+3=0 (mamy już masz równanie tej prostej w postaci ogólnej
===============
b) Stosujemy wzór na odległośc punktu od prostej
Znamy ten wzór
| |mx0 −y0−2m+3| | ||
d= | ||
| √m2+1 |
| |m*3−(−2)−2m+3| | ||
d= | ||
| √m2+1 |
| |m+5| | ||
3√2= | ||
| √m2+1 |
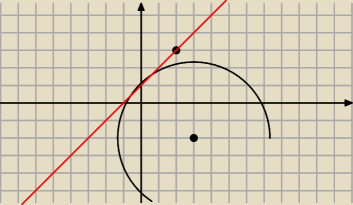
| |m+5| | |
=3√2 | |
| √m2+1 |
| 7 | ||
m1=− | ||
| 17 |
| 7 | ||
y1=− | (x−2)+3 | |
| 17 |
| 7 | 14 | |||
y1=− | x+ | +3 | ||
| 17 | 17 |
| 7 | 14 | |||
y1= − | x+3 | |||
| 17 | 17 |
 Spieszyłem sie żeby zdązyc
Czy do tej pory wszystko jest zrozumiałe dla Ciebie skąd co sie bierze ?
Spieszyłem sie żeby zdązyc
Czy do tej pory wszystko jest zrozumiałe dla Ciebie skąd co sie bierze ?


| |Ax0+By0+C| | ||
d= | ||
| √a2+b2 |
| |m*x0+(−1)*y0+−2m+3| | ||
d= | a (−1)21 | |
| √m2+(−1)2 |

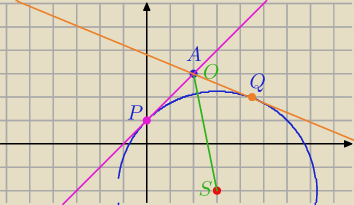 A=(2,3)
AS=√12+52=√26
x2=(√26)2−R2=26−18=8 − kwadrat długości stycznej
Równanie okręgu: O(A, r=2√2)
(x−2)2+(y−3)2=8
3)
Punkty styczności:
(x−3)2 + (y+2)2 = 18
(x−2)2+(y−3)2=8
A=(2,3)
AS=√12+52=√26
x2=(√26)2−R2=26−18=8 − kwadrat długości stycznej
Równanie okręgu: O(A, r=2√2)
(x−2)2+(y−3)2=8
3)
Punkty styczności:
(x−3)2 + (y+2)2 = 18
(x−2)2+(y−3)2=8
| 60 | 25 | |||
(P=(0,1) Q=( | , | ) | ||
| 13 | 13 |
 Zaraz sobie to wydrukuję .
A dla koleżanki moze takie
Znajdz równania stycznych do oktręgu o równaniu
(x−1)2+(y+1)2=25
i przechodzących przez punkt A=(6,9)
Zaraz sobie to wydrukuję .
A dla koleżanki moze takie
Znajdz równania stycznych do oktręgu o równaniu
(x−1)2+(y+1)2=25
i przechodzących przez punkt A=(6,9)
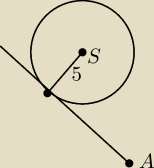 W tym przykładzie wyszło mi tylko jedno a, tym samym tylko jedna styczna, nie wiem gdzie to
zepsułam
y=a(x−x0)+y0
y−9=a(x−6)
y−9=ax−6a
ax−y−6a−9=0
|a+1−6a−9|√a2 +1 =5
−5a−8√a2 +1 =5
|−5a−8|=5√a2 +1 /2
25a2+80a+64=25a2 +5
80a=−59
a=−5980
−5980x−y−6(−5980)−9=0
−5980x−y+35480−9=0
y=−5980x−36680
W tym przykładzie wyszło mi tylko jedno a, tym samym tylko jedna styczna, nie wiem gdzie to
zepsułam
y=a(x−x0)+y0
y−9=a(x−6)
y−9=ax−6a
ax−y−6a−9=0
|a+1−6a−9|√a2 +1 =5
−5a−8√a2 +1 =5
|−5a−8|=5√a2 +1 /2
25a2+80a+64=25a2 +5
80a=−59
a=−5980
−5980x−y−6(−5980)−9=0
−5980x−y+35480−9=0
y=−5980x−36680
| |Ax0+By0+C| | ||
d= | ||
| √A2+B2 |
| |Ax0+By0+C| | ||
d= | ||
| √A2+B2 |
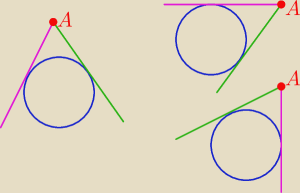 Z punktu A poza okręgiem można zawsze poprowadzić dwie styczne
1) obydwie styczne są postaci y=ax+b
2) tylko jedna jest postaci y=ax+b
to druga postaci y=yA
lub druga postaci x=xA
Z punktu A poza okręgiem można zawsze poprowadzić dwie styczne
1) obydwie styczne są postaci y=ax+b
2) tylko jedna jest postaci y=ax+b
to druga postaci y=yA
lub druga postaci x=xA
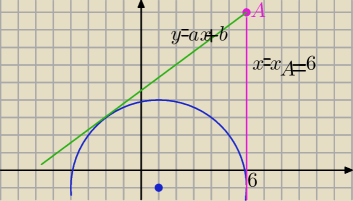
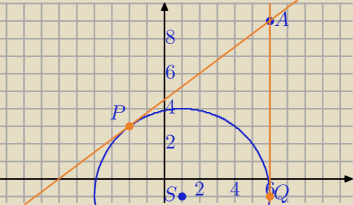 1) Znajdz równania stycznych do okręgu o równaniu
(x−1)2+(y+1)2=25 , R=5
i przechodzących przez punkt A=(6,9)
|AS|2=52+102=125
P,Q− punkty styczności
2) x2=|AS|2−R2− kwadrat dł. stycznej
x2=125−25=100=102
O(A, r=10)
(x−6)2+(y−9)2=100
3) Punkty styczności:
(x−6)2+(y−9)2=100 i (x−1)2+(y+1)2=25
P=(−2,3), Q=(6.−1)
4) styczne:
AQ: A=(6,9), B=(6,−1)⇔ x=6 i (y∊R) − prosta || OY
,
AP: A= (6,9) , (−2,3)
1) Znajdz równania stycznych do okręgu o równaniu
(x−1)2+(y+1)2=25 , R=5
i przechodzących przez punkt A=(6,9)
|AS|2=52+102=125
P,Q− punkty styczności
2) x2=|AS|2−R2− kwadrat dł. stycznej
x2=125−25=100=102
O(A, r=10)
(x−6)2+(y−9)2=100
3) Punkty styczności:
(x−6)2+(y−9)2=100 i (x−1)2+(y+1)2=25
P=(−2,3), Q=(6.−1)
4) styczne:
AQ: A=(6,9), B=(6,−1)⇔ x=6 i (y∊R) − prosta || OY
,
AP: A= (6,9) , (−2,3)
| 3 | 9 | |||
a= | , b= | |||
| 4 | 2 |
| 3 | 9 | |||
y= | x+ | |||
| 4 | 2 |