Logarytmy Hubert888: Dla jakich wartości parametru m wyrażenie ma sens liczbowy dla każdej liczby rzeczywistej? log_0,5|mx² + 2√2x + m + 1| Według odpowiedzi jest rozpatrywany warunek: |mx² + 2√2x + m + 1|>0 A dlaczego by nie wystarczyło |mx² + 2√2x + m + 1|≠0 Skoro wartość bezwzględa nigdy nie będzie mniejsza od zera

Mei Lin: Z definicji logarytmu masz ze liczba logarytmowana >0

Hubert888: Dalej nie dokońca rozumiem, bo przecież jeśli dka wartości bezględnej wykluczylibyśmy wartość zero To zawsze bedzie >0

Aruseq: |a|>0 ⇔ a≠0 ⇔ |a|≠0 − to równoważne warunki

.: Hubert. Z logicznego punktu widzenia oba zapisy są równoznaczne i oczywiście można by było zapisać ≠0 Dlaczego nie zapisano... jednym z powodów jest konsekwencja, innym jest nie wprowadzanie niepotrzebnych wątpliwości u ucznia (dlaczego w tym przypadku jest ≠0 a przecież w innych przypadkach dajemy >0)

Hubert888: Dziękuje za wyjaśnienie

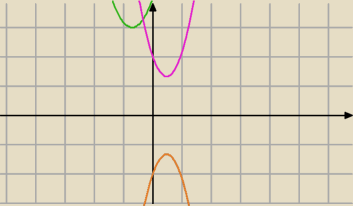
Iryt: y=|mx² + 2√2x + m + 1| 1) Musisz rozważyć dwa przypadki dla funkcji kwadratowej. m>0 i Δ<0 (zielony wykres) lub m<0 i Δ<0 ( pomarańczowy wykres, po obłożeniu wartością bezwzględną różowy wykres.) 2)

	√2
dla m=0 z dziedziny "wypada" x=−		więc nie spełnia warunków zadania.
	4

Jeśli przy niewiadomej x byłby wsp. zależny od m to należałoby taką sytuację rozważyć.