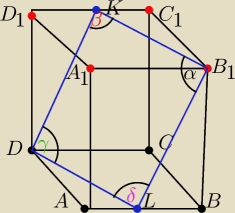
Przekrój sześcianu Mei Lin: Sześcian przecięto płaszczyzna przechodząca przez wierzchołki B₁ i D oraz środki krawędzi AB i c₁D₁. Ustalic jakiego rodzaju czworokąt otrzymano w przekroju sześcianu

.: 1. Zauważasz że wszystkie boki są równe (Pitagoras podpowiada nawet długość), 2. Wiesz ze boki są parami równoległe (dlaczego?). 3. Wystarczy sprawdzić czy jeden z kątów będzie prosty (kwadrat) czy też nie (romb) Proponuję wykorzystać przekatna DB₁ i sprawdzić czy tw. Pitagorasa zajdzie.

.: Alternatywnie w 3 możesz obliczyć |DB₁| oraz |KL| i sprawdzić czy są równe.

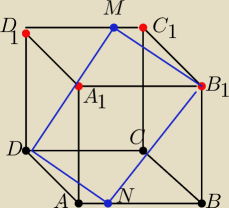
Mei Lin: Sześcian ten przecięto płaszczyzna DMB₁N Odcinki AN i C₁M stanowią trzecią część krawędzi sześcianu Ustalić jakim czworokątem jest przekrój DMC₁N

Mei Lin: Do pierwszego Sa parami równoległe bo leżą na płaszczyznach równoległych .

Mei Lin: W pierwszym będzie romb W drugim równoległobok

Mei Lin: Do tego ćwiczenia mam jeszcze takie zapytanie Jak należy przeciąć sześcian płaszczyzną by w przekroju otrzymać a) kwadrat Np płaszczyzną równoległą do podstawy b) prostokąt To wtedy płaszczyzną przekątną c) trapez Może jakas podpowiedz tutaj

ite: Jak należy przeciąć sześcian płaszczyzną by w przekroju otrzymać? a) kwadrat płaszczyzną równoległą do dowolnej ze ścian sześcianu b) prostokąt tak jak poprzednio (równoległą) lub płaszczyzną prostopadłą do dowolnej ze ścian sześcianu Już widzę, że nie są to pełne odpowiedzi. Spróbuj dodać kolejne przypadki.

Mei Lin: ite Postaram się to zrobić póżniej

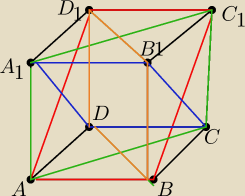
Mei Lin: Jeszcze prostokąt Przecięcie płaszczyzną BC₁D₁A Płaszczyzna A₁,DC B₁ Płaszczyzny przekątne ACC₁A₁ i DBB₁D₁.

Mei Lin: Czy to bedzie dobrze? A jeśli chodzi o ten trapez?

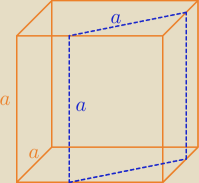
ite: Te prostokąty z 14:32 zostały już uwzględnione w odpowiedzi z 11:20. Płaszczyzny, które wymieniłeś spełniają warunek prostopadłości do którejś ze ścian sześcianu. Ja jeszcze widzę kwadraty, które powstają z przecięcia sześcianu płaszczyznami nierównoległymi do żadnej ze ścian, ale odcinającymi na ścianie (tak jak na rysunku) odcinek o długości krawędzi sześcianu. I teraz zastanawiam się, czy istnieją jeszcze jakieś inne kwadraty.

ite: A w tym podręczniku jak jest definicja trapezu? Prostokąt jest wg niej trapezem?

Mei Lin: Trapez jest w 1 części tego podręcznika . Określenie: Trapezem nazywamy taki czworokąt ,który ma tylko jedną parę boków równoległych

Mei Lin: A jeśli chodzi o trapez?

Jolanta: Co to za podręcznik? Trapez to czworokąt,który ma co najmniej jedną parę boków równoległych Trapezami sa prostokąty,rownolegloboki

.: Z komórki pisze więc rysować nie bede Natomiast jeśli miałby to być trapez NIE BĘDĄCY prostokątem lub rownoleglobokiem (czyli także nie kwadrat i romb) to Spójrz na rysunek z 14.54 teraz 'przesun' górny bok w stronę wierzchołka lub w stronę przekątnej górnej ściany. I już masz trapez równoramienny. Uwaga − − − nie możesz przekroczyć poza przekatna, bo wtedy przekrój nam przechodzi w sześciokąt.

Mei Lin: Jolu Geometria dla samouków .Cz1 Planimetria Jest to okreslenie Teraz korzystam z części 2 Stereometria Dzięki wredulus

.: A co do kwadratu i prostokąta to bym jednak szedł w 'płaszczyzna prostopadła do jednej że scian' ten warunek załatwia nam zostało będziemy mieli cztery katy proste oraz parami równe boki (czyli na pewno mamy prostokąt) i raczej wyczerpuje wszystkie możliwości. Co do tego aby na pewno był kwadrat, to poza sprawdzeniem boków, nie widzę sposobu.

ite: wredulusie płaszczyzny, o których piszesz 12:29 raczej nie wyczerpują wszystkich możliwości. Nie uwzględniają tych kwadratów "objeżdżających po krawędziach" sześcian, które próbowałam opisać 14:54.

Mei Lin: https://zapodaj.net/plik-yEaspmuO7K Skan z ksiązki gdzie o to pytają .Może to nie aż tak trudne

ite: wredulusie juz widzę na rysunku z 14:54 prostopadłość nawet do dwóch ścian i bład w tym, co napisałam o 23:28

ite: Mei Lin polecenie 3 na tym skanie rozumiem tak, że trzeba podać przykładowe przecięcie spełniające podane warunki. Ale znalezienie wszystkich możliwych rozwiązań jest ciekawsze.

wredulus_pospolitus: @ite szczerze −−− pisząc 12:29 patrzyłem przede wszystkim na Twój rysunek z 14:54 więc się mocno zdziwiłem jak napisałeś, że tego nie obejmuje

ite: mylić się jest rzeczą ludzką (i częstą : )

wredulus_pospolitus: ale jak patrzę na to co napisałem odnośnie trapezu −−− to też źle napisałem ... w sensie niekoniecznie będzie trapez równoramienny (on będzie tylko jeżeli kwadrat z 14:54 był równoległy do przekątnej podstawy)