Parametry optymalizacja, zmiana nawiasu przy dziedzinie Lodomir: Dla jakiej wartości parametru m odwrotność sumy odwrotności pierwiastków (niekoniecznie różnych) równania x² + 2(m+2)x + m² − 4m = 0 jest największa. Robię to zadanie z rozwiązaniami i generalnie ogarnąłem wszystko poza jedną rzeczą. W f(m) dziedziną jest <−1/2, + nieskończoność) \ {0, 4}, ale w pochodnej f'(m) dziedziną jest (−1/2, + nieskończoność) \ {0,4} Skąd ta zmiana z zamkniętego na otwarty

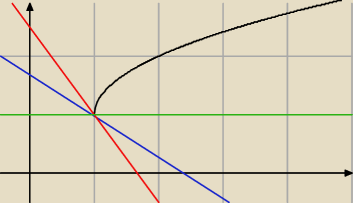
wredulus_pospolitus: dziedzina pochodnej jest ZAWSZE zapisywana w postaci przedziału otwartego. Dlaczego? Wynika to z tego co reprezentuje sobą pochodna w punkcie. Wartość pochodnej funkcji f(x) w punkcie x_o = tgα gdzie α jest kątem nachylenia STYCZNEJ do funkcji f(x) w punkcie x_o Co za tym idzie −−−> jeżeli mamy funkcję której dziedzina to [a,b) dla x_o = a istnieje NIESKOŃCZENIE WIELE prostych, które będą 'styczne' do funkcji f(x), co za tym idzie −> pochodna w tymże punkcie nie może istnieć (bo powinna być tylko jedna wartość pochodnej dla x_o=a). Przykład f(x) = √x−1 + 1 ... zauważ, że dla x_o = 1 możesz narysować nieskończenie wiele prostych, które będą styczne do wykresu f(x). W zależności od tego jaką definicję stycznej do krzywej przyjmiemy możemy uzyskać 0, 2 lub nieskończenie wiele stycznych w tymże właśnie punkcie.

wredulus_pospolitus: Ze względu na te problemy w punktach skrajnych, niemalże wszystkie definicje i twierdzenia w analizie dotyczące funkcji, mają przedział otwarty (a,b).