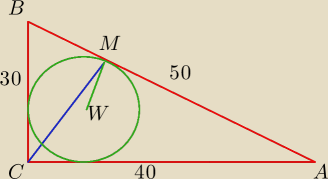
 Dany jest trójkąt prostokątny ABC, w którym |BC|=30, |AC|=40, |AB|=50.
Punkt W jest środkiem okręgu wpisanego w ten trójkąt.
Okrąg wpisany w trójkąt ABC jest styczny do boku AB w punkcie M.
Oblicz długość odcinka CM.
Dany jest trójkąt prostokątny ABC, w którym |BC|=30, |AC|=40, |AB|=50.
Punkt W jest środkiem okręgu wpisanego w ten trójkąt.
Okrąg wpisany w trójkąt ABC jest styczny do boku AB w punkcie M.
Oblicz długość odcinka CM.
| 40 * 30 | |
= 600 | |
| 2 |
| 30 + 40 + 50 | |
* r = 60r | |
| 2 |
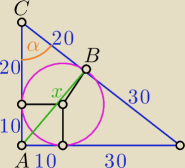
| 30 + 40 − 50 | 30 | 3 | ||||
wprost ze wzoru mamy, że r = | = 10 cos(α) = | = | ||||
| 2 | 50 | 5 |
| 3 | ||
z tw. Carnota w ΔABC: x2 = 302 + 202 − 2*30*20* | ⇔ x = ...  | |
| 5 |