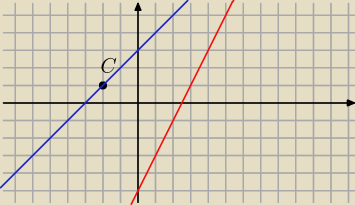
 czerwona to y=2x−5 y=x+3 niebieska to jedna z wysokości
skoro to symetralna to punkt A bedzie obrazem punktu C względem tej prostej
Wyznacz ten punkt A
Potem pomyśl troche
Skoro wysokośc przechodzi przez punkt C to musi być prostopadła do boku AB
czerwona to y=2x−5 y=x+3 niebieska to jedna z wysokości
skoro to symetralna to punkt A bedzie obrazem punktu C względem tej prostej
Wyznacz ten punkt A
Potem pomyśl troche
Skoro wysokośc przechodzi przez punkt C to musi być prostopadła do boku AB
 C=(−2,1)
y=2x−5 symetralna AC (czerwona
y=x+3 wysokośc przechodząca przez punkt C (niebieska
Równanie prostej prostopadłej do y=2x−5 i przechodzącej przez punkt C =(−2,1 ) ma postac
C=(−2,1)
y=2x−5 symetralna AC (czerwona
y=x+3 wysokośc przechodząca przez punkt C (niebieska
Równanie prostej prostopadłej do y=2x−5 i przechodzącej przez punkt C =(−2,1 ) ma postac
| 1 | ||
y=− | (x+2)+1 | |
| 2 |
| 1 | ||
y=− | x | |
| 2 |
| 1 | ||
Współrzędne punktu (S) przecięcia prostych y=− | x i y=2x−5 | |
| 2 |
| 1 | ||
− | x=2x−5 | |
| 2 |
| 5 | ||
− | x=−5 | |
| 2 |
| 1 | ||
y=− | x y=−1 | |
| 2 |
| xC+xA | ||
xS= | ||
| 2 |
| yC+yA | ||
yS= | ||
| 2 |
| xA+xB | ||
xD= | ||
| 2 |
| yA+yB | ||
yD= | ||
| 2 |