Ostrosłup john: Podstawą ostrosłupa prostego ABCS jest trójkąt prostokątny ABC o przyprostokątnych AC i BC, gdzie |AC|=6 i |BC|=8. Wyokość tego ostrosłupa jest równa 12. Oblicz tangensy kątów nachylenia ścian ACS i BCS do płaszczyzny podstawy.

kerajs: W ostrosłupie prostym wszystkie krawędzie boczne są równe. Spodek wysokości to środek przeciwprostokątnej podstawy. (Ten ostrosłup to połowa ostrosłupa o podstawie prostokątnej ABCD)

	H
tg α=		=12/4
	|BC|/2

	H
tg β=		=12/3
	|AC|/2

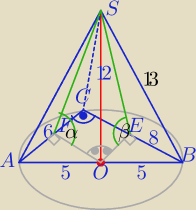
Mila: O− środek AB OE||AC, OF||BC | OE|=3, |OF|=4 pł. ACS

	12
tgα=		=3,
	4

Pł. BCS

	12
tgβ=		=4
	3

O wiele prościej i lepiej widać na rysunku wg propozycji kerajsa .