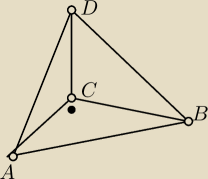
Trójkąt prostokątny Bo_ra: W trójkącie prostokątnym ABC kąt C jest kątem prostym . Z wierzchołka C wyprowadzono odcinek CD prostopadły do płaszczyzny trójkąta ABC. Punkt D połączono z punktami A i B. Znależć długości odcinków AD i BD mając dane przyprostokątne AC=7cm, BC=10cm i długośc 0odcinka CD=24cm. Odcinek CD jest prostopadly zarówno do AC jaki i do BC Zatem trójkaty ACD i BCD sa prostokątne W trójkata ACD AD²=AC²+CD² AD=√49+576=25cm W trójkącie BCD BD²=BC²+CD² BD=√100+576=26cm Nastepne polecenie jest takie Znależć od odległość punktu D od środka odcinka AB AB=√1301

1		√1301
	AB=
2		2

jak znależc ta odleglość?

wredulus_pospolitus: Najłatwiej (moim zdaniem) będzie wprowadzić układ współrzędnych. C początkiem układu. Wtedy A ma współrzędne (7,0,0) ; B ma współrzędne (0,10,0) Więc środek odcinka AB ma współrzędne (3.5 ; 5 ; 0) nazwijmy go E) stąd |CE| = mamy |CD| ... stąd |DE| =

Mila:

	1
|CE|=		|AB|
	2

Bo_ra: Dzień dobry Milu Więc tak .

	1
|CE}=		|AB| jako środkowa
	2

Więc ta odległość punktu D od środka (E) odcinka AB wyznaczę z trójkąta prostokątnego CDE bo CD będzie prostopadła do CE . Więc policzę długość odcinka DE. wredulus również dzięki

Mila: Zgadza się.