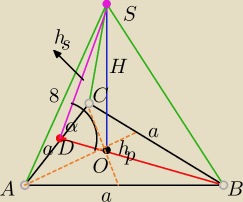
Ostrosłup Bo_ra: Wysokość ściany bocznej ostrosłupa prawidłowego trójkątnego jest nachylona do płaszczyzny podstawy pod kątem 30^o . Oblicz długość krawędzi podstawy tego ostrosłupa jeśli długość jego krawędzi bocznej wynosi 8 |AS|=8 |∡SDB|=α= 30^o −− kąt nachylenia wysokości ściany bocznej do płaszczyzny podstawy h_p−wysokość postawy ΔABC H−wysokość ostrosłupa h_s− wysokośc ściany bocznej ΔASC

	1
|DO|=		hp
	3

Niby proste ale jak wykorzystac dlugośc krawedzi ściany bocznej . mam model przed oczami

chichi:

|OD|
	= cos30o, stąd uzależnisz hs od dłg. a, następnie tw. Pitagorasa w ΔADS i po
hs

ptokach

Bo_ra: Dzięki. Proszę sprawdz jeszcze to https://matematykaszkolna.pl/forum/420750.html

Bo_ra:

	√3
cos30o=
	2

	a√2
hp=
	2

	1		1		a√3		a√3
|OD|=		hp=		*		=
	3		3		2		6

	|OD|
cos300=
	hs

	|OD|
hs=
	cos30o

	a√3		2		a		1
hs=		*		=		=		a
	6		√3		3		3

W trójkącie prostokatnym SDA

	1
|SD|=hs=		a
	3

|SA|=8

	1
|DA|=y=		a
	2

h_s²+y²=8²

1		1
	a2+		a2=64
9		4

13
	a2=64
36

	64*36
a2=
	13

	2304
a=√
	13

	48		48√13
a=		=
	√13		13

Prosze o sprawdzenie

Bo_ra:

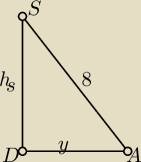
pele: koszmarny rysunek (krawędzie niewidoczne rysujemy linią przerywaną) Szkic:

	8
H>0, H2 + 12H2 = 64 ⇒ H =
	√13

	1		8		48
a − długość krawędzi podstawy,		a√3 = 3H√3 ⇒ a = 2*3*		=
	2		√13		√13

Bo_ra: czyli wyszło mi tak samo jak Tobie .Dzięki