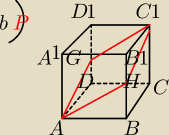
Oblicz pole przekroju sześcianu przedstawionego na rysunku poniżej, jeżeli wiado Sigma: Oblicz pole przekroju sześcianu przedstawionego na rysunku poniżej, jeżeli wiadomo, że krawędź sześcianu ma długość 6cm. Mam problem z przykładami b i c b)Płaszczyzna przekroju przechodzi przez wierzchołki A i C1 oraz punkty G i H będące odpowiednio środkami krawędzi DD1 i BB1D. Nie rozumiem czemu to nie jest kwadrat skoro kąty w środku tego przekroju są proste, a nawet jeśli to nie jest kwadrat, to jak to wtedy rozwiązać? c) Płaszczyzna przekroju przechodzi przez przekątną podstawy DB i tworzy z tą podstawą kąt 60 stopni Tutaj w o gole tego nie rozumiem, w sensie wiem ze to trapez rownoramienny ale dalej nie i wysokosc jego mi wyszla 6√2

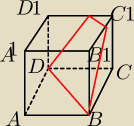Sigma: c)

Sigma: w b) to środek BB1 nie BB1D

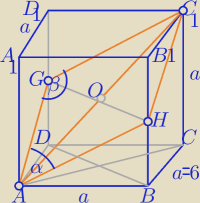Mila: b) |AC₁|=a√3=6√3 AHC₁G− czworokąt o równych bokach ( romb czy kwadrat?)

	1		5
|AH|2=a2+		a2=		a2
	4		4

	√5
|AH|=		a=3√5
	2

Możesz się przekonać na kilka sposobów. Np. (6√3)²=(3√5)²+(3√5)²−2*3√5*3√5 cosβ

	1
cosβ=−		− kąt rozwarty
	5

	1
cosα=		− kąt ostry
	5

2)

	1
Pprzekroju=		*a√3*a√2
	2

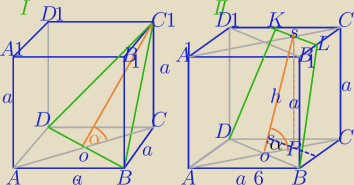Mila: 1)|AC|=a√2, |AC|=6√2, |OC|=3√2

	6		2
tgα=		=		=√2
	3√2		√2

α₀≈54,74^o I) Analiza Dla α∊(0,α₀> przekrój jest Δ Równoramiennym, ||) dla α∊(α₀,90^o> przekrój jest trapezem 60^o>α₀ 2) W ΔOPS:

	|SP|		6
sin(60o)=		=
	|OS|		h

√3		6
	=
2		h

h=4√3

	1		|OP|
cos(60o)=		=
	2		4√3

|OP|=2√3

	1
|OC|=		|AC|=3√2
	2

|SC|=|PC|=3√2−2√3 ΔKLC∼ΔD₁B₁C Dokończ. Jeśli dalej Cię to interesuje to odezwij się.