maturalne
maturzysta: Udowodnij, że x2 + 4x + 5 > 0 dla każdej liczby rzeczywistej x.
6 lut 21:20
matura:
x2+4x+4+1 = (x+2)2+1 >0 dla każdego x∊ℛ
6 lut 21:27
om:
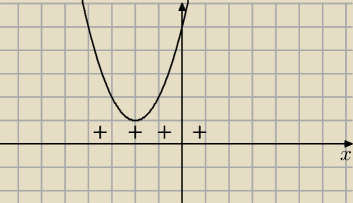
II sposób
Δ= −4<0 brak miejsc zerowych parabola cała nad osią Ox
to x
2+4x+5 >0 dla każdego x rzeczywistego
6 lut 21:35
maturzysta: Dzięki! A można graficznie? Narysować y = x2 oraz y = − 4x−5 i pokazać, że funkcja liniowa
jest poniżej kwadratowej?
6 lut 21:40
maturzysta:
6 lut 22:19
Jolanta: y=x2+4x+5 to równanie które opisuje parabole y=x2 przesunięta wzdłuż osi x oraz wzdłuż osi y.
Nie ma tutaj prostej Potrafisz napisać jak ta parabola jest przesunieta ?
6 lut 22:22
chichi:
nierówność z polecenia jest równoważna nierówności x
2 > −4x − 5, więc narysował wykresy lewej
i prawej strony
7 lut 00:21