katy
zul: Trójkąt ABC jest równoboczny, przy czym na boku BC leżą takie punkty K, L, że BK=KL=LC. Znaleźć
miary kątów BAK oraz KAL.
6 lut 19:28
żulik:
Wartości przybliżone
|∡BAK|≈19o i |∡KAL|≈22o
6 lut 20:03
Bo_ra:
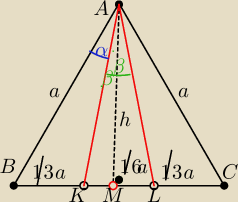
Moja propozycja
|AB|=|BC|=|AC|=a
| | 1 | |
Z treści zadania jest że |BK|=|KL|=|LC|= |
| a |
| | 3 | |
∡|BAK|=α
∡|KAL|=2β
Takze z tresci zadania wynika że |KA|=|KL|
Wobec tego ΔKLA jest trójkatem równoramiennym
To oznacza że |AM| =h jest wysokościa zarówno tego ΔKLA jak i ΔABC
dzieli ona odcinek KL na polowę
| | 1 | | 1 | | √3 | |
tgβ= |
| a*U{2}{a√3= |
| = |
| ≈0,192 |
| | 6 | | 3√3 | | 9 | |
β≈11
o
∡|KAL|=2β≈22
o
β+α=30
o
∡|BAK|=α=30
o−11
o≈19
o
6 lut 20:58
NN:
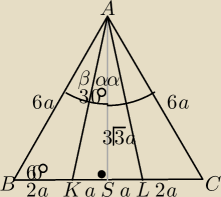
Z własności trójkąta o kątach 90
o,30
o,60
o
|BC|=6a , |AS|=3
√3a , |BS|=3a i |KS|=a
| | a | |
tgα= |
| = U{√3}{9 ⇒α≈11o |
| | 3√3a | |
α+β=30
o ⇒ β≈19
o
|∡BAK|≈19
o , |∡KAL|=2α≈22
o
6 lut 21:25
 Moja propozycja
|AB|=|BC|=|AC|=a
Moja propozycja
|AB|=|BC|=|AC|=a
 Z własności trójkąta o kątach 90o,30o,60o
|BC|=6a , |AS|=3√3a , |BS|=3a i |KS|=a
Z własności trójkąta o kątach 90o,30o,60o
|BC|=6a , |AS|=3√3a , |BS|=3a i |KS|=a