ostrosłup - kąt dwuścienny matematycznyswir: Cześć, proszę o pomoc bo już się całkiem pogubiłam. Podstawą ostrosłupa jest kwadrat, a spodek wysokości znajduje się w jednym z wierzchołków tego kwadratu. Wiedząc, że wysokość ostrosłupa jest równa krawędzi podstawy, wyznacz: wyznaczone mam: a) tg kąta nachylenia najdłuższej krawędzi bocznej ostrosłupa do płaszczyzny podstawy (wyznaczyłam jako √2/2) b) cos kąta między najdłuższą krawędzią boczną ostrosłupa a krawędzią podstawy o wspólnym wierzchołku (wyznaczyłam jako √3/3) c) miarę kąta nachylenia ścian bocznych, które nie zawierają wysokości ostrosłupa, do płaszczyzny podstawy (wyznaczyłam 45 stopni) i problem sprawia mi wyznaczenie d) miary kąta dwuściennego między dwiema ścianami bocznymi o największej powierzchni który dokładnie jest to kąt i jak go wyliczyć?

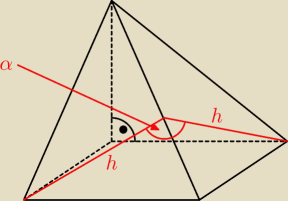
wredulus_pospolitus: szukamy miary tego kąta. Procedura:

	a*a√2
1. Wyznaczamy pole ściany bocznej o największym polu (P =		) gdzie 'a' to długość
	2

podstawy 2. Najdłuższa krawędź boczna (z pitagorasa jeżeli jeszcze nie wyliczyłaś) ... = √3a

	2P		a√6
3. h =		=
	√3a		3

	a√6		a√6		a√6
4. Z tw. cosinusów: (√2a)2 = (		)2 + (		)2 − 2(		)2cosα
	3		3		3

	1
cosα = 1 −		−−−> α =
	2

wredulus_pospolitus: wskazówka:

	√2
1. dla ułatwienia pisz h =		nie musisz później skracać
	√3

2. w sytuacji: x² = y² + y² − 2(y²)cosα możemy zauważyć, że będziemy mieli:

	x2
x2 = 2y2(1−cosα) −−−> cosα = 1 −		... podstawiamy iiii ... zauważamy że źle
	2y2

policzyłem (ale juz sama odnajdziesz mój błąd w rachunkach).

matematycznyswir: dlaczego h = ^2P_√3a ?

matematycznyswir: cofam! właśnie zauważyłam, że h można obliczyć z wzoru h = ^ab_c , a później podstawić do to twierdzenia cosinusów. dziękuję

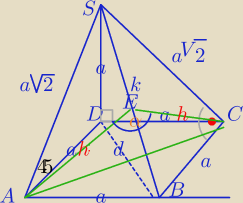
Mila: 1) d=a√2 k²=3a² z ΔSDB i obu Δ k=a√3 ΔSCB≡ΔSAB − 2)

	a2√2
PΔ{SCB}=
	2

1		a2√2
	a√3h=
2		2

√3h=a√2 h=U{a√2{√3} 3) 2a²=2h²−2h² cosα a²=h²(1−cosα)

	3
1−cosα=a2*
	2a2

	3
1−cosα=
	2

	1
cosα=−
	2