oblicz objętość
Shadowex: Kąt rozwarcia stożka ma miarę 30 stopni a jego podstawa ma pole równe (18−9√3)π cm2. Oblicz
objętość tego stożka
8 sty 21:35
wredulus_pospolitus:
1. Masz jego pole podstawy −−−> masz promień podstawy.
2. Masz promień podstawy −−−> masz średnicę podstawy.
3. Masz średnicę podstawy + kąt rozwarcia stożka + pamiętasz tw. cosinusów −−−> masz tworzącą
l.
4. Masz tworzącą l + masz promień podstawy + pamiętasz tw. Pitagorasa −−−> masz wysokość
stożka.
5. Masz wysokość stożka + Pp −−−> masz objętość stożka.
8 sty 23:05
Shadowex: no tak, znam tworzącą l oraz promień podstawy, problem pojawia się, kiedy próbuje to
powymnażać, pojawiają się jakieś zagnieżdzone pierwiastki i wygląda to kiepsko
8 sty 23:34
Shadowex: wysokość też wychodzi mi jakaś dziwna
8 sty 23:35
wredulus_pospolitus:
to pokaż swoje obliczenia ... a na przyszłość − nie wrzucaj zadania (jakby czekając na gotowca)
tylko przedstaw W CZYM TKWI PROBLEM I POKAŻ OBLICZENIA
8 sty 23:42
Mila:
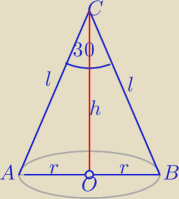
P
◯=π r
2
1)
π r
2= (18−9
√3)π
r
2=18−9
√3
r
2=9*(2−
√3)
r=3
√2−√3
2r=6
√2−√3
2)
|AB|=2r
Tw. cosinusów
(2r)
2=36*(2−
√3)
36(2−
√3)=l
2+l
2−2l
2*cos (30
o)
36*(2−
√3)=2l
2−l
2*
√3
36*(2−
√3)=l
2*(2−
√3)
l
2=36
l=6
3) h:
6
2=(3
√2−√3)
2+h
2
h
2=36−9(2−
√3)=18+9
√3
h=3
√(2+√3) i licz objętość
Jeśli przeszkadza Ci ten pierwiastek, to zrób tak:
| √2+√3 | | √2 | | √4+2√3 | | √(1+√3)2 | | 1+√3 | |
| * |
| = |
| = |
| == |
| |
| 1 | | √2 | | √2 | | √2 | | √2 | |
9 sty 15:51
Min.Edukacji: Voilla
I masz gotowiec😁
9 sty 21:46
Shadowex: Dziękuję wielkie, następnym razem wrzucę obliczenia, nie wiedziałem jak to forum funkcjonuję,
dziękuję za zwrócenie uwagi.
10 sty 00:48
Mila:
10 sty 00:56