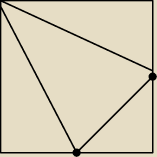
 W kwadracie ABCD punkt E jest środkiem boku AB, a punkt F środkiem boku BC. Pole trójkąta DEF
jest równe 18 cm². Oblicz pole kwadratu ABCD. Wykonaj rysunek.
Jak można rozwiązać to zadanie nie używając x?
Ja zrobiłam tak:
P kwadratu = 4 • x2
P trójkątów = 2,5 x2
1,5 x2 = 18
x= 2 √3
P kwadratu = 4 • 2 • √3 • 2 • √3 = 16 • 3 = 48 cm2
W kwadracie ABCD punkt E jest środkiem boku AB, a punkt F środkiem boku BC. Pole trójkąta DEF
jest równe 18 cm². Oblicz pole kwadratu ABCD. Wykonaj rysunek.
Jak można rozwiązać to zadanie nie używając x?
Ja zrobiłam tak:
P kwadratu = 4 • x2
P trójkątów = 2,5 x2
1,5 x2 = 18
x= 2 √3
P kwadratu = 4 • 2 • √3 • 2 • √3 = 16 • 3 = 48 cm2
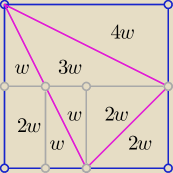 P=18= 6w ⇒ w=3
P□=16w = 16*3=48
P=18= 6w ⇒ w=3
P□=16w = 16*3=48
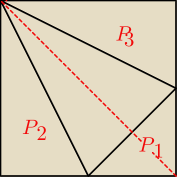 Rozwiązanie zapisane SKRÓTOWO
Rozwiązanie zapisane SKRÓTOWO  P2 = P3
Jako, że DE i DF to środkowe trójkątów ABD i BCD, to mamy:
PΔ + P1 = P2 + P3 −−−> 2(PΔ + P1) = P□
P2 = P3
Jako, że DE i DF to środkowe trójkątów ABD i BCD, to mamy:
PΔ + P1 = P2 + P3 −−−> 2(PΔ + P1) = P□
| 1 | ||
P1 = | P□ | |
| 8 |
| 2 | 8 | 8 | ||||
P□ − | P□ = 2PΔ −−−> P□ = | PΔ = | *18 = 48  | |||
| 8 | 3 | 3 |
| 1 | 1 | |||
P= | P+ | P+18 | ||
| 2 | 8 |
