Trójkat Stary rok : W trójkącie równoramiennym ABc w którym |AC|=|BC| i |∡ACB|=α poprowadzono dwusieczną kąta BAC przecinającą bok BC w punkcie D i okazało się ze |AD|=|AB|=|CD|. Wyznacz miarę kąta α i wykaż że

	α		√5−1
sin		=
	2		4

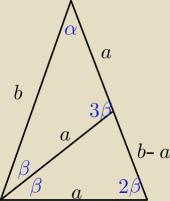
wredulus_pospolitus: 1. zauważ, że ΔADC jest równoramienny −−−> α = β −−−> α = 36^o 2. więc musimy wyznaczyć ile wynosi sin18^o i teraz pytanie do Ciebie −−−> jak wyznaczyć sin18^o

Stary rok : Wyznacze sin36 ^o a potem zastosuje wzór połówkowy

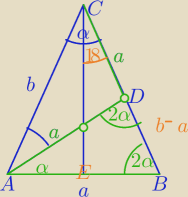
Mila: 1) 5α=180^o α=36^o 2) ΔADB∼ΔABC

a		b−a
	=
b		a

a²=b²−ab a²+ab−b²=0

	b(√5−1)
a=
	2

	a/2		b(√5−1)   2*2		√5−1
sin(18o)=		=		=
	b		b		4

Najlepiej przyjąć b=1, wtedy łatwiejsze (?) rachunki)

Stary rok : dziękuje

Nowy Rok nadchodzi: Jako,że "Stary Rok" lubi trygonometrię to:

	1
wie,że : cos36o*sin18o=		i cos36o=1−2sin218o
	4

podstawienie : sin18^o= x x∊(0,1) więc 4x(1−2x²)=1 8x³−4x+1=0 w(1/2) =0 ale sin18^o≠1/2 (2x−1)(4x²+2x−1)=0

	√5−1
Δ=2√5 to x =		>0
	4

	√5−1
sin18o=
	4

=============