proszę o rozwiązanie anna: W czworokącie ABCD przekątne przecinają się w punkcie E oraz |BE | = |CE | . Przekątna BD dzieli czworokąt ABCD na trójkąt równoboczny i trójkąt równoramienny Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe. Kąt ABC ma miarę 100⁰ . P F Kąt AEB ma miarę 70⁰ . P F

Yorgan: Anna, radziłabym Ci skorzystać z zajęć z korepetytorem z matematyki, aby rozwiązać takie problemy. Tutaj, na Mathemie https://mathema.me/pl/tutors/, możesz wybrać korepetytora, który Ci pomoże i wyjaśni cechy rozwiązywania takich problemów. Nie czekaj na ostatnią chwilę, by nadrobić zaległości. Zacznij już teraz rozwijać swoje umiejętności matematyczne z pomocą ekspertów z Mathema. Dzięki temu nie tylko podniesiesz swoje oceny, ale także zbudujesz solidne podstawy pod przyszłą karierę.

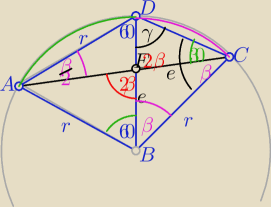
Eta: Czy ten rys. wystarczy ? 1/ P 100^o 2/ F 80^o

anna: czworokąt nie był narysowany w kole zadanie nr 15 z Próbnego Egzaminu Ósmoklasisty z Matematyki Zestaw przygotowany przez serwis zadania.info 27 kwietnia 2024

Eta: Można na nim opisać okrąg o środku B i promieniu r=|AB|= |BD|= |BC| ( bo ΔABD równoboczny o boku długości "r" i ΔBCD równoramienny o ramionach długości "r" Czy teraz już jasne?

Eta: @ anna ( jesteś uczennicą? czy nauczycielką?

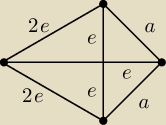
wredulus_pospolitus: @Etuś ... W Twoim rozwiązaniu brakuje mi wyjaśnienia dlaczego to ABD jest równoramienny (ja wiem, ale autorka raczej nie będzie wiedziała) Drugą sprawę ... do której już się mogę przyczepić ... to dlatego założyłaś, że tak wygląda trójkąt BCD. Dlaczego nie rozpatrzyłaś sytuacji, gdzie czworokąt ABCD jest deltoidem. Przecież on także spełnia warunki zadania.

wredulus_pospolitus: a w tym przypadku oczywiście a = e√2 i mam F i F

Eta: "wredusku" tak wygląda rys. do zadania 15 https://zadania.info/d1855/89553

.: Skoro tak wygląda rysunek, to mea culpa