Zadanie z działu "Funkcja kwadratowa". Mulder: W trójkąt ostrokątny ABC, w którym |AB| = a oraz wysokość |CD| = h wpisujemy prostokąty tak, że jeden bok prostokąta zawiera się w boku AB, a dwa pozostałe wierzchołki należą do boków AC oraz BC. Podaj wymiary prostokąta o największym polu. Nie wiem, jak to rozwiązać, a siedziałem nad tym długo. Poproszę o wskazówkę.

Pluto: Szukaj trójkątów podobnych

Pluto:

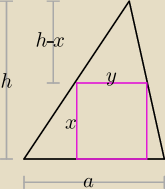
a		h		a
	=		⇒ y = a −		x, x∊(0, h) i y∊(0, a)
y		h − x		h

	a
pole prostokąta P = xy = −		x2 + ax
	h

	a
P(x) = −		x2 + ax, wykresem P(x) jest parabola skierowana ramionami w ... (itd)
	h

Mulder: Dziękuję, Pluto.