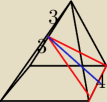
 Obwód podstawy i obwód ściany bocznej ostrosłupaprawidłowego czworokątnego są równe 16, oblicz
pole przekroju tego ostrosłupa płaszczyzną zawierającą krawędź podstawy i środek rozłącznej z
nią krawędzi bocznej. Mam problem z wyliczeniem wysokości tego przekroju, jakaś pomoc...
Obwód podstawy i obwód ściany bocznej ostrosłupaprawidłowego czworokątnego są równe 16, oblicz
pole przekroju tego ostrosłupa płaszczyzną zawierającą krawędź podstawy i środek rozłącznej z
nią krawędzi bocznej. Mam problem z wyliczeniem wysokości tego przekroju, jakaś pomoc...
 Bo raczej nie taki co
narysowałeś.
Druga sprawa −−− jeżeli jednak podstawą jest kwadrat, to przekrój NIE BĘDZIE trójkątem, a
prostokątem.
Bo raczej nie taki co
narysowałeś.
Druga sprawa −−− jeżeli jednak podstawą jest kwadrat, to przekrój NIE BĘDZIE trójkątem, a
prostokątem.
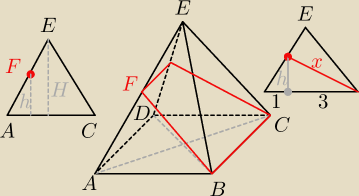 dziecko ... trochę pokory ... jeżeli tak byś zrobił/−a rysunek to bym nic nie mówił
1. Obliczasz krawędź podstawy
2. Obliczasz wysokość ściany bocznej
3. Tworzysz trójkąt prostokątny o bokach: 'wysokość ostrosłupa, połowa długości krawędzi
podstawy, wysokość ściany bocznej' w celu wyznaczenia wysokości ostrosłupa
4. Robisz rysunek sytuacyjny (patrz na lewo od ostrosłupa). Na jego podstawie wyznaczasz 'h'.
5. Robisz następny przekrój (patrz na prawo od ostrosłupa) równoległy do AB, prostopadły do
podstawy, przechodzący przez E. x to szukana wysokość tego TRAPEZU.
6. Masz wysokość trapezu, masz dłuższą podstawę, (mam nadzieję że) masz krótszą podstawę −−−>
liczysz pole trapezu
dziecko ... trochę pokory ... jeżeli tak byś zrobił/−a rysunek to bym nic nie mówił
1. Obliczasz krawędź podstawy
2. Obliczasz wysokość ściany bocznej
3. Tworzysz trójkąt prostokątny o bokach: 'wysokość ostrosłupa, połowa długości krawędzi
podstawy, wysokość ściany bocznej' w celu wyznaczenia wysokości ostrosłupa
4. Robisz rysunek sytuacyjny (patrz na lewo od ostrosłupa). Na jego podstawie wyznaczasz 'h'.
5. Robisz następny przekrój (patrz na prawo od ostrosłupa) równoległy do AB, prostopadły do
podstawy, przechodzący przez E. x to szukana wysokość tego TRAPEZU.
6. Masz wysokość trapezu, masz dłuższą podstawę, (mam nadzieję że) masz krótszą podstawę −−−>
liczysz pole trapezu
 Mila help
Mila help 



 dzięki wredulus za pomoc, ale nie tedy droga.
dzięki wredulus za pomoc, ale nie tedy droga.
 NIE BEDZIE RÓWNORAMIENNY,
NIE BEDZIE RÓWNORAMIENNY, 



 https://odrabiamy.pl/matematyka/ksiazka-10757/strona-125/zadanie-471499
MILA help
https://odrabiamy.pl/matematyka/ksiazka-10757/strona-125/zadanie-471499
MILA help 
 !
!












 !
!
 Drugi problem masz taki: nie jesteś w stanie zrobić porządnego rysunku
Drugi problem masz taki: nie jesteś w stanie zrobić porządnego rysunku  Trzeci problem masz taki: nie słuchasz / czytasz co się do Ciebie pisze
Trzeci problem masz taki: nie słuchasz / czytasz co się do Ciebie pisze 
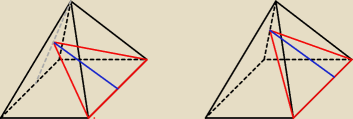 Twój rysunek sugeruje sytuację po lewej .... zapewne chciałaś narysować sytuację po prawej.
Tak czy siak ... TO NIE JEST PRZEKRÓJ
Twój rysunek sugeruje sytuację po lewej .... zapewne chciałaś narysować sytuację po prawej.
Tak czy siak ... TO NIE JEST PRZEKRÓJ  Przez ostrosłup prawidłowy czworokątny.
Jak byś wzięła do ręki nóż i zrobiła takie cięcie to ostrosłup NIE ZOSTAŁBY podzielony na dwie
części
Przez ostrosłup prawidłowy czworokątny.
Jak byś wzięła do ręki nóż i zrobiła takie cięcie to ostrosłup NIE ZOSTAŁBY podzielony na dwie
części
 "Łapiemy o co chodzi"
"Łapiemy o co chodzi"  Robisz gówniany
rysunek i jeszcze bardziej gówniany przekrój
Robisz gówniany
rysunek i jeszcze bardziej gówniany przekrój  Wredulus i "." to tak sama osoba (komputer vs komórka).
Dyskusja jak wodospad bo o 17:49 dostałaś sposób rozwiązania, którego nie byłaś w stanie
przyjąć bo uważasz, że przekrój inaczej wygląda (któraś z wersji pokazana o 21:03).
Tu cała dyskusja po 17:49 jest tylko po to aby uświadomić Tobie, że przekrojem przez ostrosłup
prawidłowy czworokątny (gdzie przekrój przechodzi przez krawędź podstawy) będzie trapez a nie
żaden trójkąt i Twoje upieranie się przy tym, że wcale tak nie będzie powoduje tą dyskusję.
Wredulus i "." to tak sama osoba (komputer vs komórka).
Dyskusja jak wodospad bo o 17:49 dostałaś sposób rozwiązania, którego nie byłaś w stanie
przyjąć bo uważasz, że przekrój inaczej wygląda (któraś z wersji pokazana o 21:03).
Tu cała dyskusja po 17:49 jest tylko po to aby uświadomić Tobie, że przekrojem przez ostrosłup
prawidłowy czworokątny (gdzie przekrój przechodzi przez krawędź podstawy) będzie trapez a nie
żaden trójkąt i Twoje upieranie się przy tym, że wcale tak nie będzie powoduje tą dyskusję.










 ! Eta i Mila MISTZROSTWO ŚWIATA
! Eta i Mila MISTZROSTWO ŚWIATA  !
!
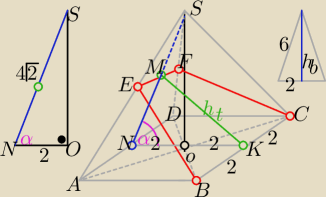 Przekrojem jest [C[trapez równoramienny]
o podstawach 4 i 2
|NM|=2√2
Przekrojem jest [C[trapez równoramienny]
o podstawach 4 i 2
|NM|=2√2
| √2 | ||
cosα= | , α= 45o | |
| 2 |
| √2 | ||
ht 2= 42+(2√2)2−2*4*2√2* | ||
| 2 |
 bo nie napisałaś
zapewne
pole przekroju = pole trapezu=..............
bo nie napisałaś
zapewne
pole przekroju = pole trapezu=..............
| √2 | ||
cosα= | ||
| 4 |
 Nadal nie potrafisz policzyć pola tego przekroju? Pomimo tego, że Eta dała Ci na
srebrnej tacy dane które masz wrzucić do wzoru?
A czemu z Etą nie dywagujesz odnośnie tego, że przekrojem nie jest trapez (równoramienny) tylko
trójkąt?
Nadal nie potrafisz policzyć pola tego przekroju? Pomimo tego, że Eta dała Ci na
srebrnej tacy dane które masz wrzucić do wzoru?
A czemu z Etą nie dywagujesz odnośnie tego, że przekrojem nie jest trapez (równoramienny) tylko
trójkąt?